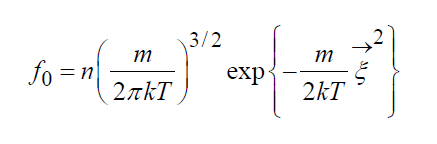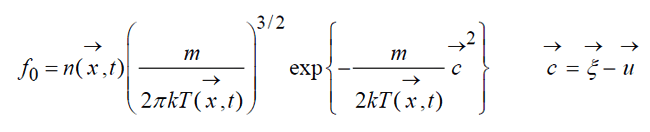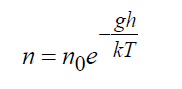|
| Испарение и конденсация |
Пленочное кипение |
Сверхтекучий гелий |
Эксперименты | События | Библиотека |
Испарение и конденсацияПленочное кипениеСверхтекучий гелийЭксперименты События и мероприятияБиблиотекаСправочные данные Больцманиада• Людвиг Больцман. Биографическая справка.• Ученый и учитель• Именные достижения• Философия молекулярно-кинетического подхода• Фундаментальное наследие Л.БольцманаХейке Камерлинг-ОннесКриогениус |
Людвиг Больцман: Именные достиженияЗакон излучения Стефана-БольцманаСогласно закону Стефана – Больцмана плотность интегрального полусферического излучения E0 зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры T: (1)
Постоянная Стефана-БольцманаСтефана – Больцмана постоянная σ0 – физическая постоянная, входящая в закон, определяющий объемную плотность равновесного теплового излучения абсолютно черного тела: (2)
Исторически закон Стефана-Больцмана был сформулирован раньше закона излучения Планка, из которого он вытекает как следствие. Закон Планка устанавливает зависимость спектральной плотности потока излучения E0 от длины волны λ и температуры T: (3)
где λ – длина волны, м; с=2,998 108 м/с – скорость
света в вакууме; Т – температура тела, К;
Постоянная БольцманаФизическая постоянная k, равная отношению универсальной газовой постоянной R=8314Дж/(кг×K) к числу Авогадро NA=6,022×10261/(кг×моль): (4)
Статистика БольцманаЧисло различных конфигураций системы из N частиц для данного набора чисел ni (число частиц, находящихся в i-том состоянии, которому соответствует энергия ei) пропорционально величине: (5)
Величина W есть число способов распределения N частиц по энергетическим уровням. Если справедливо соотношение (6) то считается, что исходная система подчиняется статистике Больцмана. Набор чисел ni, при котором число W максимально, встречается наиболее часто и соответствует наиболее вероятному распределению.
Физическая кинетика – микроскопическая теория процессов в статистически неравновесных системах. Описание большого числа частиц может успешно осуществляться вероятностными методами. Для одноатомного газа состояние совокупности молекул определяется их координатами и значениями проекций скоростей на соответствующие координатные оси. Математически это описывается функцией распределения, характеризующей вероятность пребывания частицы в данном состоянии: (6)
есть ожидаемое число молекул в
объеме d Газ БольцманаЕсли осредненной по времени потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией, то газ называется идеальным. Идеальный газ называется газом Больцмана, если отношение длины пробега молекул в этом газе к характерному размеру течения L конечно, т.е. (7)
т.к. длина пробега обратно пропорциональна nd2(n – числовая плотность 1/м3, d – диаметр молекулы, м).
H-функция БольцманаВеличину (8)
называют H-функцией Больцмана для единицы объема, которая связана с вероятностью обнаружения системы из молекул газа в данном состоянии. Каждому состоянию соответствуют определенные числа заполнения шестимерных пространственно-скоростных ячеек, на которые может быть разбито фазовое пространство рассматриваемых молекул. Обозначим W вероятность того, что в первой ячейке рассматриваемого пространства окажется N1 молекул, во второй N2 и т.д. С точностью до постоянной, определяющей начало отсчета вероятности, правомерно соотношение: (9)
где
H-теорема Больцмана(10)
Принцип БольцманаБольцмана принцип устанавливает связь между энтропией S физической системы и термодинамической вероятностью W её состояния: (11)
Кинетическое уравнение Больцмана(печатается по изданию: Коган М.Н. Динамика разреженного газа. – М.: Наука, 1967.) Общий вид КУБ: (12)
где (13)
Уравнение (12) с интегралом (13) получено для столкновения молекул, при которых не возникает тангенциальных сил, т.е. сталкивающиеся частицы считаются идеально гладкими. В процессе
взаимодействия внутренняя энергия молекул не меняется, т.е. предполагается, что
эти молекулы являются идеально упругими. Рассматриваются две группы молекул,
имеющих до соударения друг с другом (столкновения) скорости
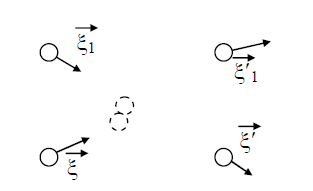
Рис. 1. Столкновение двух молекул. В (13) входят два параметра,
характеризующие расположение сталкивающихся молекул друг относительно друга: b
и ε; b – прицельное расстояние,
т.е. наименьшее расстояние, на которое сблизились бы молекулы при отсутствии
взаимодействия (рис. 2); ε называют
угловым параметром столкновений (рис. 3). Интегрирование по b от 0 до ¥ и
по от 0 до 2p (два внешних интеграла в
(12)) охватывает всю плоскость силового взаимодействия перпендикулярно вектору
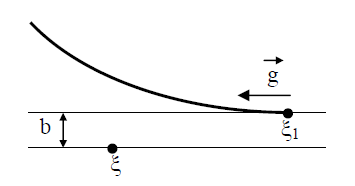
Рис. 2. Траектория движения молекул.
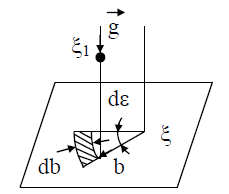
Рис. 3. Рассмотрение взаимодействия молекул в цилиндрической системе координат: z, b, ε Кинетическое уравнение Больцмана выведено при следующих допущениях и предположениях. 1. Считается, что происходит в основном столкновения двух молекул, т.е. роль столкновений одновременно трех и большего числа молекул незначительна. Это допущение позволяет использовать для анализа одночастичную функцию распределения, которая выше названа просто функцией распределения. Учет столкновения трех молекул приводит к необходимости использования в исследовании двухчастичной функции распределения. Соответственно анализ существенно усложняется. 2.
Предположение о молекулярном хаосе. Оно выражается в том, что вероятности
обнаружения частицы 1 в фазовой точке 3.
Равновероятны столкновения молекул с любым прицельным расстоянием, т.е. функция
распределения не меняется на диаметре взаимодействия. Необходимо отметить, что
анализируемый элемент Распределение Максвелла-БольцманаРавновесное состояние газа описывается абсолютным Максвелловским распределением, которое является точным решением кинетического уравнения Больцмана: (14)
где m – масса молекулы, кг. Общее локально-максвелловское распределение иначе называемое распределение Максвелла-Больцмана: (15)
в том случае, когда газ движется
как целое со скоростью
Формула Больцмана барометрическаяВ поле тяготения Земли точное решение уравнения Больцмана показывает: (16)
где n0= плотность у поверхности Земли, 1/м3; g – ускорение силы тяжести, м/с2; h – высота, м. Формула (16) является точным решением кинетического уравнения Больцман либо в безграничном пространстве, либо при наличии границ, не нарушающих этого распределения, при этом температура также должна оставаться постоянной. Эта страница оформлена Пузиной Ю.Ю. при поддержке Российского Фонда Фундаментальных Исследований – проект №08-08-00638. Следующая страница: Философия молекулярно-кинетического подхода
|
|
Испарение и конденсация
Пленочное кипение
Сверхтекучий гелий
Эксперименты События Библиотека Справочники Больцманиада Камерлинг-Оннес Криогениус |
|
© Криофизика.рф 2006-2021. Молекулярно-кинетическая теория. Научные публикации. Испарение и конденсация. Плёночное кипение. Сверхтекучий гелий. |
о проекте условия использования |
контакты карта сайта |
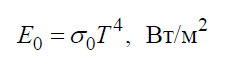
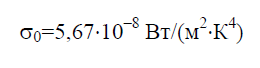
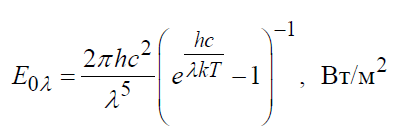
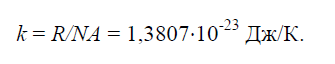
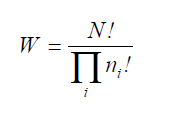
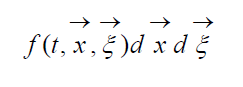
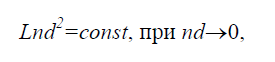
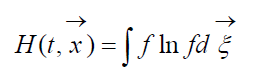
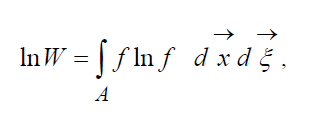 ,
,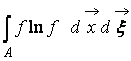 – H-функция области
пространства А, занятой газом. Из (9) видно, что W и H
взаимосвязаны, т.е. изменение вероятности состояния приводит к соответствующей
эволюции H функции.
– H-функция области
пространства А, занятой газом. Из (9) видно, что W и H
взаимосвязаны, т.е. изменение вероятности состояния приводит к соответствующей
эволюции H функции.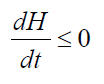
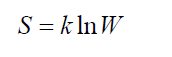
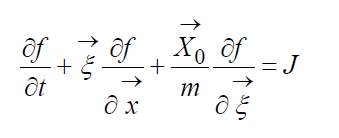
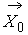 – массовая сила, обусловленная наличием различных полей (гравитационного,
электрического, магнитного), действующая на молекулу;
– массовая сила, обусловленная наличием различных полей (гравитационного,
электрического, магнитного), действующая на молекулу; 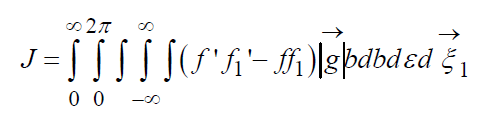
 . Потенциалы
взаимодействия, используемые при вычислении интеграла столкновений, являются
сферически симметричными, т.е.
. Потенциалы
взаимодействия, используемые при вычислении интеграла столкновений, являются
сферически симметричными, т.е.