Рост подогреваемой паровой полости в капилляре,
заполненном Не-II, при турбулентном течении нормального компонента и вихревом
сверхтекучем движении*
П.В.
Королев
Московский
энергетический институт
Постановка задачи
Рассматривается
рост парового пузыря в круглом цилиндрическом микроканале (капилляре) диаметром
d, по которому циркулирует сверхтекучий гелий. На некотором ограниченном
участке канала, имеющем длину lw,
сопоставимую с его диаметром, к гелию II через стенки
канала от источника теплоты (охлаждаемого объекта) поступает тепловой поток,
линейная плотность которого – 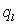 . Суммарная мощность, подводимая к
гелию II, очевидно, равна . Суммарная мощность, подводимая к
гелию II, очевидно, равна 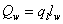 . За исключением участка подвода
теплоты боковая поверхность канала адиабатически изолирована. При этом
выполняется условие: . За исключением участка подвода
теплоты боковая поверхность канала адиабатически изолирована. При этом
выполняется условие:
(1)
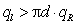 , ,
где 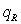 – плотность теплового потока, при
которой происходит переход от пленочного кипения к режиму непосредственного
контакта Не-II с греющей поверхностью, т.е.
восстановительная тепловая нагрузка в стесненных условиях (в капилляре),
отличающаяся от аналогичной величины при кипении в большом объеме. В некоторый
момент времени по каким-либо причинам возникает следующая аварийная ситуация:
тепловая мощность, выделяемая охлаждаемым объектом, увеличивается настолько,
что плотность теплового потока со стенок канала становится выше «пиковой»
тепловой нагрузки – плотность теплового потока, при
которой происходит переход от пленочного кипения к режиму непосредственного
контакта Не-II с греющей поверхностью, т.е.
восстановительная тепловая нагрузка в стесненных условиях (в капилляре),
отличающаяся от аналогичной величины при кипении в большом объеме. В некоторый
момент времени по каким-либо причинам возникает следующая аварийная ситуация:
тепловая мощность, выделяемая охлаждаемым объектом, увеличивается настолько,
что плотность теплового потока со стенок канала становится выше «пиковой»
тепловой нагрузки 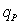 , при которой происходит образование
пара: , при которой происходит образование
пара:
(2)
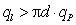 , ,
и одновременно с этим
прекращается циркуляция гелия II в канале. В результате
процесса парообразования в микроканале возникает паровой пузырь, который растет
и перекрывает все сечение микроканала, как показано на рисунке 1. Образуется
паровая пробка, имеющая длину l. Пусть отношение
длины капилляра к его диаметру достаточно велико, и паровая пробка за
относительно большое время после начала роста успевает вырасти лишь до длины,
не превышающей нескольких процентов от длины капилляра. Кроме того, примем, что
в рассматриваемом случае тонкая пленка жидкости, отделяющая паровую полость от
стенок канала, полностью испаряется. Некоторое время спустя тепловой поток от
охлаждаемого объекта уменьшается до прежней величины 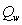 . Поскольку эта величина
превышает восстановительную тепловую нагрузку, то паровая пробка не
схлопывается. Рост паровой пробки будет продолжаться, при этом тепловой поток,
поступающий в паровую полость со стенок канала, будет затрачиваться на нагрев
пара, совершение работы по увеличению объема полости и испарение гелия II с межфазных поверхностей (менисков). Испарение Не-II прекратится, как только давление в паровой пробке станет
выше, чем давление по линии насыщения при температуре границ раздела фаз (эти
положения обосновываются далее). Процесс испарения закончится еще до того, как
тепловая нагрузка уменьшится до начального значения . Поскольку эта величина
превышает восстановительную тепловую нагрузку, то паровая пробка не
схлопывается. Рост паровой пробки будет продолжаться, при этом тепловой поток,
поступающий в паровую полость со стенок канала, будет затрачиваться на нагрев
пара, совершение работы по увеличению объема полости и испарение гелия II с межфазных поверхностей (менисков). Испарение Не-II прекратится, как только давление в паровой пробке станет
выше, чем давление по линии насыщения при температуре границ раздела фаз (эти
положения обосновываются далее). Процесс испарения закончится еще до того, как
тепловая нагрузка уменьшится до начального значения 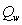 . В этом случае масса пара
не будет изменяться по окончании формирования паровой пробки, а часть теплоты,
поступающей в паровую полость, будет отводиться через межфазные поверхности
пар-жидкость в гелий II. Плотность теплового потока,
распространяющегося в гелии II, обозначим как q (см. рис. 1). Пусть величина q
такова, что реализуется вихревой режим сверхтекучего движения и турбулентный
режим течения нормального компонента. Для такой ситуации ставится задача
сформулировать условия, выполнение которых позволит предотвратить дальнейший
рост паровой пробки и обеспечить ее схлопывание. . В этом случае масса пара
не будет изменяться по окончании формирования паровой пробки, а часть теплоты,
поступающей в паровую полость, будет отводиться через межфазные поверхности
пар-жидкость в гелий II. Плотность теплового потока,
распространяющегося в гелии II, обозначим как q (см. рис. 1). Пусть величина q
такова, что реализуется вихревой режим сверхтекучего движения и турбулентный
режим течения нормального компонента. Для такой ситуации ставится задача
сформулировать условия, выполнение которых позволит предотвратить дальнейший
рост паровой пробки и обеспечить ее схлопывание.
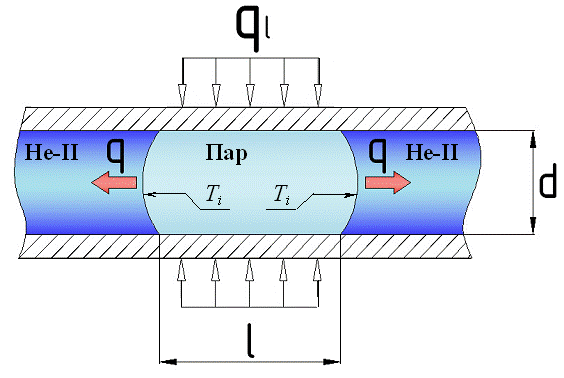
Рис. 1. Рост паровой пробки в
капилляре, заполненном Не-II, при подводе теплоты через стенку капилляра
Математическая модель
Как было
сказано выше, после завершения формирования паровой пробки часть подводимой к
пару тепловой мощности отводится через две межфазные поверхности в Не-II, а другая часть (обозначим ее как Q) затрачивается на нагрев пара и совершение работы по
увеличению объема паровой полости. Поэтому можно записать
(3)
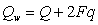 , ,
где F – площадь поперечного сечения канала.
Для
определения величины теплового потока Q, идущего
на нагрев пара и совершение работы, запишем уравнение первого начала термодинамики:
(4)
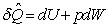 , ,
где 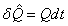 – количество теплоты, приходящее к
пару за интервал времени dt, – количество теплоты, приходящее к
пару за интервал времени dt,
dW – изменение объема
паровой полости за время dt, р – давление
пара в полости,
dU – изменение
внутренней энергии пара. Из (4) следует, что
(5)
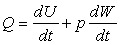 , ,
имея в виду (5), уравнение (3)
можно переписать как
(6)
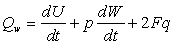 . .
Объем паровой полости W, очевидно, равен
(7)
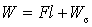 , ,
где F – площадь поперечного сечения канала, l – длина паровой пробки, Ws – объем, обусловленный
кривизной межфазных поверхностей. Вследствие симметрии задачи границы раздела
фаз движутся с одинаковыми скоростями 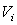 , поэтому , поэтому 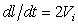 , и, следовательно,
изменение объема паровой пробки за единицу времени равно , и, следовательно,
изменение объема паровой пробки за единицу времени равно
(8)
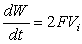 . .
Очевидно, что
(9)
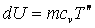 , ,
где m
– масса пара в полости, 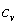 – удельная теплоемкость пара при
постоянном объеме, – удельная теплоемкость пара при
постоянном объеме,
Т” – средняя температура пара в полости. Таким образом, из (6), (8) и
(9) получается следующее уравнение:
(10)
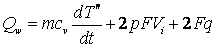 . .
Для
определения производной 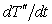 запишем уравнение состояния пара,
который будем рассматривать как идеальный газ: запишем уравнение состояния пара,
который будем рассматривать как идеальный газ:
(11)
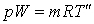 . .
где R –
индивидуальная газовая постоянная. Прямое численное решение кинетического
уравнения Больцмана (КУБ) для нестационарных задач тепломассопереноса, в
которых одна из межфазных поверхностей является границей раздела жидкой фазы и
пара [1, 2], показывает, что стационарное состояние, характеризуемое
отсутствием потока массы через эту границу, достигается за время кинетической
релаксации, имеющее порядок времени между столкновениями молекул пара. Таким
образом, как было сказано ранее, масса пара m
увеличивается на этапе формирования паровой пробки и остается постоянной на
протяжении времени ее дальнейшего роста. Выполненное моментным методом решение
стационарного КУБ для задачи о переносе теплоты через межфазную границу из пара
в жидкость показывает, что давление пара в этой ситуации всегда несколько
больше, чем давление по линии насыщения при температуре межфазной поверхности
[3, 4]. Однако, разность давлений пара и давления по линии насыщения много меньше
величин самих этих давлений, поэтому можно положить, что давление пара равно
давлению по линии насыщения: 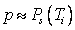 , приняв, таким образом,
квазиравновесное приближение. Поскольку эффективность теплопереноса по
сверхтекучему гелию феноменально высока даже по сравнению с жидкими металлами,
увеличение температур межфазных поверхностей , приняв, таким образом,
квазиравновесное приближение. Поскольку эффективность теплопереноса по
сверхтекучему гелию феноменально высока даже по сравнению с жидкими металлами,
увеличение температур межфазных поверхностей
пар-жидкость по мере поступления теплоты в Не-II будет
незначительным в сравнении с начальной температурой жидкого гелия,
следовательно, рост давления пара в полости также будет мал по сравнению с
начальным давлением в паровой пробке, установившимся после прекращения
испарения с межфазных поверхностей. По этой причине будем считать давление пара
в полости при ее росте приблизительно постоянным (квазиизобарный процесс).
При неизменной
массе пара в полости и постоянстве давления из уравнения (11) получается
следующая взаимосвязь изменения объема с изменением средней температуры пара:
(12)
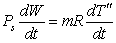 , ,
из которой, учитывая (8), можно
найти производную 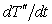 : :
(13)
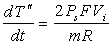 . .
Подставив
полученное выражение для производной 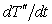 в (10) и выполнив несложные
преобразования, найдем выражение для величины плотности теплового потока в
гелии II: в (10) и выполнив несложные
преобразования, найдем выражение для величины плотности теплового потока в
гелии II:
(14)
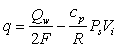 . .
где 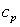 – удельная теплоемкость пара при
постоянном давлении. – удельная теплоемкость пара при
постоянном давлении.
Согласно
условиям задачи длина паровой пробки не превышает нескольких процентов длины
капилляра, следовательно, при увеличении парового объема уменьшение длины
заполненных гелием II участков капилляра всегда
существенно меньше их начальной (после возникновения пузыря) длины. Кроме того,
было принято допущение о незначительности изменения давления пара в пробке. Это
позволяет сделать предположение о квазистационарном характере течения жидкости
под действием медленно изменяющегося градиента давления. Будем считать, также
как и в работе [5], что инерционными силами можно пренебречь и в любой момент
времени жидкость движется стационарно. Квазистационарное течение гелия II в канале при вихревом сверхтекучем движении описывается
выведенным в [6] уравнением:
(15)
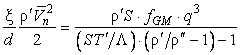 , ,
где d – диаметр капилляра;
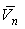 – средняя
по сечению канала скорость течения нормального компонента Не-II;
x – динамический коэффициент вязкого
трения; T’ – средняя температура жидкого гелия; fGM – функция Гортера-Меллинка при температуре T’;
Λ – удельная теплота парообразования; q – плотность теплового потока в Не-II;
S – удельная энтропия гелия II; – средняя
по сечению канала скорость течения нормального компонента Не-II;
x – динамический коэффициент вязкого
трения; T’ – средняя температура жидкого гелия; fGM – функция Гортера-Меллинка при температуре T’;
Λ – удельная теплота парообразования; q – плотность теплового потока в Не-II;
S – удельная энтропия гелия II;
ρ’ – плотность Не-II; ρ”– плотность пара при
температуре T’. В случае турбулентного режима течения нормального
компонента уравнение (15) принимает вид:
(16)
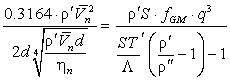 , ,
где ηn –
динамическая вязкость нормального компонента. Плотность теплового потока в
движущемся гелии II может быть выражена формулой,
полученной в [7]:
(17)
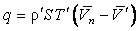 , ,
где 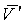 – средняя по сечению канала
скорость течения Не-II как целого. Из (17) находится
взаимосвязь – средняя по сечению канала
скорость течения Не-II как целого. Из (17) находится
взаимосвязь 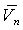 и и
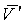 : :
(18)
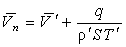 . .
Средняя по
сечению канала скорость течения жидкого гелия при росте паровой пробки равна
скорости движения межфазных поверхностей: 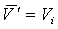 , поскольку поток массы с этих
поверхностей равен нулю. Плотность теплового потока q
определяется по формуле (14). Подставив выражения для q и , поскольку поток массы с этих
поверхностей равен нулю. Плотность теплового потока q
определяется по формуле (14). Подставив выражения для q и 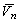 в уравнение (16) и выполнив несложные
преобразования, получаем: в уравнение (16) и выполнив несложные
преобразования, получаем:
(19)
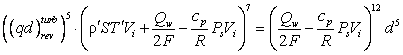 , ,
где
(20)
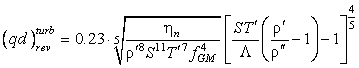 . .
– значение величины q×d, при котором происходит изменение направления течения
Не-II в капилляре, полученное в результате решения
задачи о движении перемычки (объема, ограниченного менисками) Не-II в горизонтальном микроканале при наличии продольного
теплового потока, вихревом режиме сверхтекучего движения и турбулентном
нормальном движении [6]. Умножив обе части уравнения (19) на d7 и поделив на 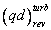 имеем: имеем:
(21)
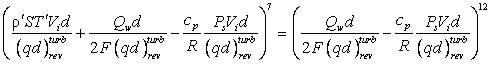 . .
Введя следующие обозначения:
(22)
 , ,
(23)
 , ,
запишем уравнение (21) как
(24)
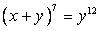 . .
Из этого уравнения выражаем х:
(25)
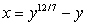 . .
Функцию 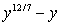 можно с неплохой точностью
аппроксимировать формулой следующего вида: можно с неплохой точностью
аппроксимировать формулой следующего вида: 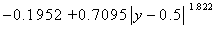 , что позволяет получить приближенную
зависимость , что позволяет получить приближенную
зависимость
у от х:
(26)
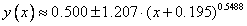 . .
Для получения же точных значений
функции y(x)
необходимо решать уравнение (25) численными методами.
Подставив в
(26) выражения (22) и (23) для х и у, соответственно, и учитывая,
что площадь сечения канала F равна
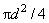 ,
приходим к формуле для определения такой величины тепловой нагрузки Qw, при которой межфазные поверхности будут
двигаться со скоростью Vi: ,
приходим к формуле для определения такой величины тепловой нагрузки Qw, при которой межфазные поверхности будут
двигаться со скоростью Vi:
(27)
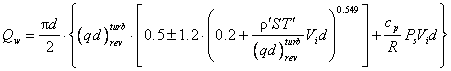 . .
Границы применимости решения
Формула (27)
применима для случаев, когда сверхтекучее движение является вихревым, а
нормальное – турбулентным при значениях числа Рейнольдса от 2000 до 104
[8]. Нижняя граница этого диапазона соответствует началу развитого
турбулентного течения нормального компонента. Сверхтекучее движение становится
вихревым, когда его скорость превышает критическую скорость 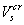 . Нормальное движение
перестает быть ламинарным, когда его скорость становится больше критической
скорости . Нормальное движение
перестает быть ламинарным, когда его скорость становится больше критической
скорости 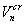 .
В работе [9], в связи с проблемой критических скоростей, отмечается:
«Критические скорости двух компонентов в He-II имеют различную природу. Для сверхтекучего компонента
критическая скорость .
В работе [9], в связи с проблемой критических скоростей, отмечается:
«Критические скорости двух компонентов в He-II имеют различную природу. Для сверхтекучего компонента
критическая скорость 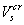 — это такая скорость, которая
необходима для возникновения турбулентности в этом компоненте. Эта
турбулентность представляет собой совокупность квантовых вихревых нитей, петель,
клубков и т.п. Для нормального компонента тоже существует критическая скорость — это такая скорость, которая
необходима для возникновения турбулентности в этом компоненте. Эта
турбулентность представляет собой совокупность квантовых вихревых нитей, петель,
клубков и т.п. Для нормального компонента тоже существует критическая скорость 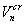 , которая связана с
переходом от ламинарного к турбулентному режиму течения, как в обычной
жидкости. Критическая скорость нормального компонента может быть рассмотрена с
позиций классической гидродинамики». , которая связана с
переходом от ламинарного к турбулентному режиму течения, как в обычной
жидкости. Критическая скорость нормального компонента может быть рассмотрена с
позиций классической гидродинамики».
Скорость течения
нормального компонента, при которой заканчивается переход от ламинарного режима
нормального движения к развитому турбулентному, таким образом, может быть
найдена из следующей формулы [8, 9]:
(28)
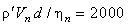 . .
Из формул (28), (18) и (14) путем несложных
преобразований получаем выражение для величины тепловой нагрузки, при
достижении которой начинается развитое турбулентное течение нормального
компонента:
(29)
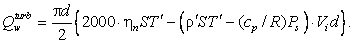
Критическая скорость 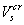 , при которой
возникают вихри, формирующие, в конце концов, клубки сверхтекучей
турбулентности, может быть определена по следующей эмпирической зависимости
[9], хорошо аппроксимирующей экспериментальные данные: , при которой
возникают вихри, формирующие, в конце концов, клубки сверхтекучей
турбулентности, может быть определена по следующей эмпирической зависимости
[9], хорошо аппроксимирующей экспериментальные данные:
(30)
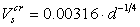 . .
В этой формуле число 0.00316 имеет размерность м5/4×с–1. Из формул (30), (18),
(14) и соотношения для плотности потока массы в гелии II
при противотоке компонентов:
(31)
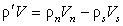
находим формулу для определения критической тепловой
нагрузки 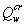 ,
при которой происходит переход к вихревому режиму сверхтекучего движения: ,
при которой происходит переход к вихревому режиму сверхтекучего движения:
(32)
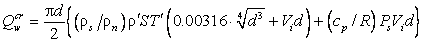 , ,
где ρs, ρn – плотность нормального и сверхтекучего компонентов Не-II, соответственно.
Из решения задачи о движении
столбика гелия II в капилляре при подводе теплоты к одной из межфазных
поверхностей, полученного с учетом неравновесных кинетических эффектов на
границах раздела фаз (более общая постановка задачи, рассмотренной в [6]),
легко выводится критерий, при выполнении которого термодинамической
неравновесностью можно пренебречь. Это условие справедливо и для исследуемой
здесь задачи о росте паровой полости. В том случае, когда учитываются
кинетические скачки давления только вблизи «теплых» межфазных поверхностей (но
не «холодных», интенсивность тепломассопереноса через которые существенно
меньше, если их площадь значительно превосходит площадь «теплых» менисков),
критерий имеет вид:
(33)
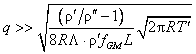 , ,
где L – длина участка капилляра (левого или правого),
заполненного гелием II. Стоящая в неравенстве (33)
величина q определяется с помощью формул (23) и
(26). Из (23) и (33) получается соотношение для оценки длины L, при которой выполняется условие (33):
(34)
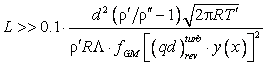 , ,
где y(x) определяется по формуле (26).
Предлагаемая
модель роста паровой пробки относительно адекватно описывает реальный процесс,
если капиллярные силы, действующие на межфазные поверхности и по порядку величины
равные 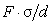 ,
пренебрежимо малы по сравнению с силами вязкого трения в рассматриваемом случае
равными ,
пренебрежимо малы по сравнению с силами вязкого трения в рассматриваемом случае
равными 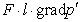 ,
даже при разной кривизне «теплых» и «холодных» межфазных границ. Градиент
давления в Не-II равен левой части уравнения (16), и
можно легко показать, что ,
даже при разной кривизне «теплых» и «холодных» межфазных границ. Градиент
давления в Не-II равен левой части уравнения (16), и
можно легко показать, что 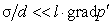 при при
(35)
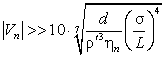 , ,
где s – поверхностное натяжение жидкости. Из формул (18), (23) и
последнего соотношения получаем следующее соотношение для оценки L, при которой силами поверхностного натяжения
можно пренебречь:
(36)
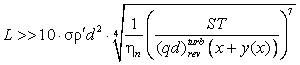 . .
Чтобы
составить представление о том, при каких длинах капилляра можно не учитывать
эффекты термодинамической неравновесности на межфазных границах и пренебречь
капиллярными силами в сравнении с силами вязкого трения, обозначим правые части
неравенств (34) и (36) как Lkin и Ls,
соответственно, и построим зависимости величин 100×Lkin и 100×Ls от величины Vi×d (см. рис. 2). Очевидно, что
условия (34) и (36) будут выполняться, если значение L
превышает 100×Lkin и 100×Ls.
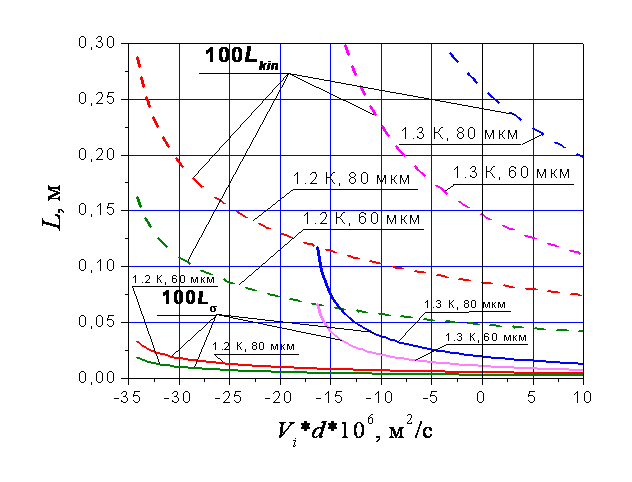
Рис. 2. Зависимости 100×Lkin и 100×Ls от величины Vi×d
При
рассмотрении рис. 2 становится очевидным, что Ls всегда меньше×Lkin
при одинаковых значениях температуры гелия II и
диаметра капилляра, поэтому представленная здесь модель эволюции паровой пробки
корректна при L >>
Lkin. Если температура Не-II не превышает 1.3 К и диаметр капилляра составляет десятки
микрометров, то условие
L > 100Lkin, как легко можно увидеть, выполняется при
L составляющей десятки сантиметров.
Результаты: графическое представление
На рис. 3
показаны рассчитанные с помощью формулы (27) зависимости величины Vi×d от отношения тепловой нагрузки к диаметру канала для
температур жидкого гелия 1.2, 1.3 и 1.4 К. Данные зависимости справедливы
только в области турбулентного нормального и вихревого сверхтекучего движения,
ограниченной на графике прямыми, построенными по формулам (29) и (32). Хорошо
видно, что при средней температуре сверхтекучего гелия в микроканале, равной
1.4 К и диаметре микроканала 400 мкм, зависимость (27) почти целиком лежит за
пределами этой области. Таким образом, полученное решение имеет физический
смысл при более низких температурах и/или меньших диаметрах капилляров. При
температуре Не-II выше 1.4 К формула (27) описывает
поведение паровой пробки только в капиллярах диаметром десятки микрометров. Как
легко можно заметить, в определенном диапазоне значений величины Qw/d скорость
межфазных поверхностей отрицательна (участки кривых ниже точек А1, А2 и А3).
Это означает, что в этом случае происходит схлопывание паровой пробки. Из
формул (27) и (20) получаем, что межфазные поверхности будут двигаться
навстречу друг другу, если
(37)
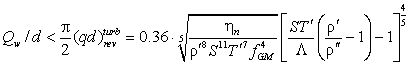 . .
В таблице 1 представлены значения величины 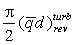 при различных
средних температурах гелия II в канале. при различных
средних температурах гелия II в канале.
Таблица 1. – Значения величины 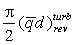 . .
|
T,
K
|
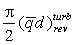 , Вт/м , Вт/м
|
|
1.20
|
2.49
|
|
1.30
|
2.10
|
|
1.40
|
1.77
|
|
1.50
|
1.47
|
|
1.60
|
1.26
|
|
1.70
|
1.00
|
Поскольку
величина 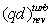 зависит
только от температуры, то условие (37) дает возможность для заданной величины
тепловой нагрузки Qw выбрать температуру Не-II
и диаметр капилляра, при которых произойдет коллапс паровой полости. зависит
только от температуры, то условие (37) дает возможность для заданной величины
тепловой нагрузки Qw выбрать температуру Не-II
и диаметр капилляра, при которых произойдет коллапс паровой полости.
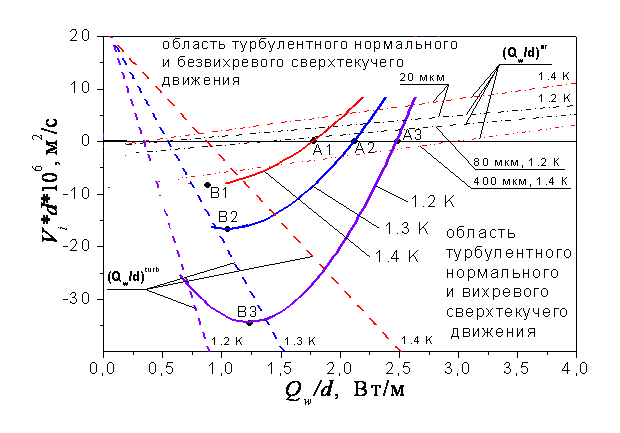
Рис. 3. Зависимости величины Vi×d от
отношения тепловой нагрузки к диаметру канала
Как видно из
рис. 3 при некотором значении Qw/d скорость уменьшения размера паровой полости
максимальна. Из формулы (27) следует, что эта скорость по абсолютной величине
равна
(38)
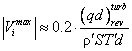 , ,
и достигается при величине Qw/d,
определяемой по формуле:
(39)
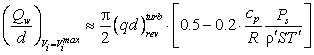 . .
Очевидно, что во избежание аварийных ситуаций в каналах теплообменников
микрокриогенного оборудования при их проектировании следует стремиться к
выполнению критерия схлопывания (37) или, еще лучше, условия (39),
обеспечивающего наиболее быстрый коллапс паровой пробки. При соблюдении этих
рекомендаций, прекращение циркуляции гелия II и
одновременное кратковременное увеличение подводимой на ограниченном участке
микроканала тепловой нагрузки не приведет к его осушению.
Следует отметить, что приведенные на рис. 2 зависимости 100×Lkin
и 100×Ls от величины Vi×d справедливы только при 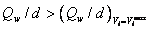 , т.е. для участков А1 – В1, А2 – В2 и
А3 – В3 изображенных на рис. 3 зависимостей Vi×d
от Qw/d,
но именно этот случай и представляет интерес для практических приложений. , т.е. для участков А1 – В1, А2 – В2 и
А3 – В3 изображенных на рис. 3 зависимостей Vi×d
от Qw/d,
но именно этот случай и представляет интерес для практических приложений.
Заключение
Проведенные расчетные исследования квазистационарного
и квазиизобарного роста подогреваемой паровой пробки в микроканале, заполненном
сверхтекучим гелием, доказывают принципиальную возможность схлопывания паровой
полости, поскольку и в этой ситуации (при незаторможенном нормальном
компоненте, турбулентном режиме движения этого компонента и вихревом сверхтекучем
движении), как и в известных опытах со «сверхщелями», возможно течение He-II к
источнику теплоты. Определены условия схлопывания паровой пробки, и условия при
которых скорость уменьшения объема пробки будет максимальной. Задача решена для
случаев, когда сверхтекучее движение является вихревым, а режим течения
нормального компонента – турбулентным. Такие режимы течения компонентов He II
реализуются при относительно высоких плотностях теплового потока, которые
реально могут встречаться в инженерной практике. Полученные результаты найдут
применение при проектировании работающего на сверхтекучем гелии
микрокриогенного оборудования, используемого для охлаждения микроэлектронных
устройств, миниатюрных инфракрасных датчиков и т.п. Представленное решение
задачи показывает, что нежелательное осушение микроканалов теплообменников,
случающееся при аварийных ситуациях, в ряде случаев может быть предотвращено.
Работа выполнена в рамках исследований по грантам
Президента Российской Федерации для государственной поддержки молодых
российских ученых МК-4372.2008.8.
СПИСОК ОБОЗНАЧЕНИЙ
Не-II – сверхтекучий гелий (гелий II);
КУБ – кинетическое уравнение Больцмана;
с – теплоемкость пара, Дж/(кг×К);
d – диаметр капилляра, м;
F – площадь сечения капилляра, м2;
fGM – функция Гортера – Меллинка, К×м5/Вт3;
L – длина участков (левого и правого) капилляра, заполненных Не-II, м;
l – текущая длина паровой пробки, м;
lw – длина участка подвода теплоты, м;
m – масса пара, кг;
p - давление, Па;
Q – тепловой поток, Вт;
q – плотность теплового потока, Вт/м2;
R – индивидуальная газовая постоянная, Дж/(кг×К);
S – энтропия гелия II, Дж/(кг×К);
T – температура, К;
t – время, с;
U – внутренняя энергия пара, Дж;
V – скорость, м/с;
W – объем паровой полости, м3;
Греческие символы:
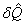 – количество теплоты, за интервал времени dt приходящее к пару, Дж; – количество теплоты, за интервал времени dt приходящее к пару, Дж;
η – динамическая вязкость жидкости, Па×с;
Λ – удельная теплота парообразования, Дж/кг;
x – динамический коэффициент вязкого трения;
ρ – плотность, кг/м3;
s – поверхностное натяжение жидкости, Н/м;
Индексы:
’ –относится к параметрам жидкости;
” –относится к параметрам пара;
cr – critical критические значения величин;
i – interface относится к «теплым» межфазным поверхностям;
kin – связано с эффектами термодинамической неравновесности;
l – удельная величина на единицу длины капилляра;
n – normal относится к нормальной компоненте He-II;
P – peak относится к пиковой тепловой нагрузке;
p – при постоянном давлении;
R – recovery относится к восстановительной тепловой нагрузке;
rev – reverse значение величины при котором происходит обращение течения гелия II;
s – superfluid относится к сверхтекучей компоненте; saturated значение на линии насыщения;
Список литературы
1.
Kryukov A.P. and Shishkova I.N. Transfer
phenomena in vapour film on the interphase of superfluid helium in terrestrial
conditions and in Microgravity // Proc. Joint Xth European and VIth Russian
Symp. on Physical Sciences in Microgravity. Moscow. Russia. 1997. Vol. 1. P.
341–348.>>
2. Ястребов
А.К., Крюков А.П. Решение уравнения Больцмана для задачи теплопереноса в
паровой пленке при пленочном кипении // Труды Третьей Российской национальной
конференции по теплообмену. М.: Издательство МЭИ, 2002. Т. 8. С. 148–151.>>
3.
Муратова Т.М., Лабунцов Д.А. Кинетический анализ процессов
испарения и конденсации // Теплофизика высоких температур. 1969. Т. 7. №5. С.
959–976.>>
4. Labuntsov D.A. and Kryukov A.P. Analysis of intensive evaporation
and condensation // International Journal of the Heat Mass Transfer. 1979.
Vol. 22. P. 989.>>
5. Земских
В.И., Крылова М.В. Макроскопические характеристики движения границы раздела фаз
в единичном капилляре с учетом капиллярных сил // Механика жидкости и газа.
1998. №1. С. 188–190.>>
6. П.В.
Королев. Течение Не-II в горизонтальном капилляре при
наличии продольного теплового потока и вихревом режиме сверхтекучего движения
// Труды XVI Школы-семинара молодых ученых и
специалистов под руководством академика РАН А.И. Леонтьева. В 2-х т. М.:
Издательский дом МЭИ, 2007. Т.1. С. 182–185.>>
7.
Королев П.В., Крюков А.П. Движение сверхтекучего гелия в
капилляре с паром при наличии продольного теплового потока // Вестник МЭИ.
2002. №1. С. 43–46.>>
8.
К Takamatsu et al. Numerical study flow and heat
transfer of superfluid helium in capillary channels // Cryogenics. 1997. Vol.
37. Num. 11. P. 829–835.>>
9.
S. W. Van Sciver. Helium Cryogenics. New York: Plenum Press. 1986.– 423 p.>>
* Королев П.В. Рост
подогреваемой паровой полости в капилляре, заполненном Не-II,
при турбулентном течении нормального компонента и вихревом сверхтекучем
движении. // Труды Третьей международной конференции «Тепломассообмен и
гидродинамика в закрученных потоках». 21-23 октября 2008г. Москва. – Сборник
трудов на компакт-диске. –S221.
Следующая страница: Об одном эксперименте по кипению сверхтекучего гелия на цилиндрическом нагревателе
| 
![]() зависит
только от температуры, то условие (37) дает возможность для заданной величины
тепловой нагрузки Qw выбрать температуру Не-II
и диаметр капилляра, при которых произойдет коллапс паровой полости.
зависит
только от температуры, то условие (37) дает возможность для заданной величины
тепловой нагрузки Qw выбрать температуру Не-II
и диаметр капилляра, при которых произойдет коллапс паровой полости.
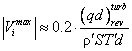 ,
, 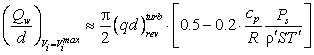 .
.![]() , т.е. для участков А1 – В1, А2 – В2 и
А3 – В3 изображенных на рис. 3 зависимостей Vi×d
от Qw/d,
но именно этот случай и представляет интерес для практических приложений.
, т.е. для участков А1 – В1, А2 – В2 и
А3 – В3 изображенных на рис. 3 зависимостей Vi×d
от Qw/d,
но именно этот случай и представляет интерес для практических приложений.![]() – количество теплоты, за интервал времени dt приходящее к пару, Дж;
– количество теплоты, за интервал времени dt приходящее к пару, Дж;
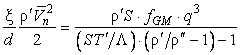 ,
,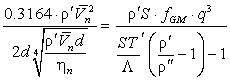 ,
,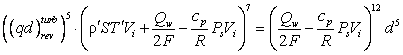 ,
,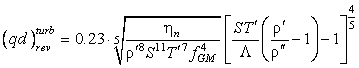 .
. 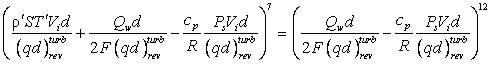 .
. ,
,  ,
, 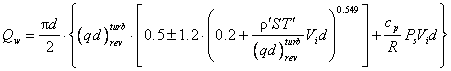 .
. 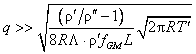 ,
,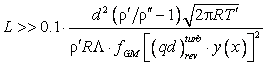 ,
,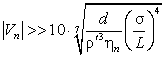 ,
,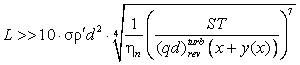 .
. 
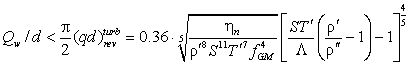 .
.