|
| Испарение и конденсация |
Пленочное кипение |
Сверхтекучий гелий |
Эксперименты | События | Библиотека |
Испарение и конденсацияПленочное кипениеСверхтекучий гелий• Течение Не-II в горизонтальном капилляре • Рост подогреваемой паровой полости в капилляре, заполненном Не-II• Об одном эксперименте по кипению сверхтекучего гелия на цилиндрическом нагревателе• Определение взаимосвязи радиуса паровой плёнки с проницаемостью пористой структуры при кипении сверхтекучего гелия при условиях микрогравитации• Течение гелия-II в канале с пористой вставкой при безвихревом сверхтекучем движении• Эксперимент по кипению He-II на цилиндрическом нагревателе внутри пористой структурыЭксперименты События и мероприятияБиблиотекаСправочные данные БольцманиадаХейке Камерлинг-ОннесКриогениус |
Течение Не-II в горизонтальном капилляре при наличии продольного теплового потока и вихревом режиме сверхтекучего движения *П.В. Королев Московский энергетический институт 1. ВВЕДЕНИЕРабота посвящена разработке моделей стационарного движения объема Не-II в капилляре при турбулентном (вихревом) режиме течения сверхтекучего компонента, формулировке соответствующего математического описания и расчетным исследованиям данного процесса. В инженерной практике корректное описание теплопереноса при течении He-II необходимо для прогнозирования нежелательного осушения каналов теплообменных аппаратов. Полученные результаты могут быть использованы в процессе разработки методик определения условий, при которых исключена возможность осушения микроканалов криогенных систем охлаждения, что, в свою очередь, позволит обеспечить устойчивое функционирование различных устройств, охлаждаемых сверхтекучим гелием. 2. ПОСТАНОВКА ЗАДАЧИРассматривается стационарное движение объема гелия II в круглом цилиндрическом капилляре диаметром d (см. рис. 1.). Объем He-II имеет известную длину l. В гелии II каким-либо образом генерируется тепловой поток, распространяющийся вдоль оси канала. Например, тепловой поток может подводиться к одной из межфазных поверхностей или возникать вследствие разности температур, созданной между концами канала. Задача решается для ситуаций, в которых эффектами термодинамической неравновесности на границах раздела фаз можно пренебречь (квазиравновесное приближение). Это означает, что температуры пара в полостях принимаются равными температурам межфазных поверхностей, а давления пара – давлениям соответствующим этим температурам по линии насыщения. Известная плотность теплового потока обозначена как q. Боковая поверхность канала адиабатически изолирована, т.е. поток теплоты через стенку канала считается нулевым. Плотность теплового потока в He-II такова, что реализуется вихревой режим течения сверхтекучего компонента. Принимается, что режим течения нормального компонента может быть как ламинарным, так и турбулентным. Форма межфазных поверхностей не имеет значения в том случае, если капиллярные силы пренебрежимо малы по сравнению с силами вязкого трения, несмотря на то, что границы раздела фаз имеют разную кривизну. Например, при ламинарном режиме течения нормального компонента движении такая ситуация имеет место, если выполняется условие: (1)
где Капиллярными силами можно пренебречь и в том случае, если в заполненных паром участках на стенках канала существует не испаряющаяся под действием теплового потока пленка Не-II микроскопической или макроскопической толщины, и, вследствие этого, кривизна межфазных поверхностей приблизительно одинакова, так что капиллярные силы, действующие на мениски, почти полностью взаимно компенсируются. Принимается, что теплофизические свойства Не-II не зависят от температуры. Предполагается, что инерционными силами можно пренебречь, и в любой момент времени жидкость движется стационарно со скоростью, соответствующей давлениям на границах раздела фаз, и текущей длине перемычки l. Требуется определить скорости движения нормального компонента и всей жидкости в целом.
3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬСогласно двухскоростной гидродинамике Л.Д. Ландау Не-II можно представить состоящим из двух компонентов: нормального, имеющего плотность (2)
(3)
В этих формулах Умножив обе части уравнения (3) на (4)
получаем для случая стационарного течения He-II уравнение следующего вида (5)
где Умножив обе части уравнения (2) на (6)
Поскольку, капиллярными силами пренебрегается, то, очевидно, что перепад давления в He-II равен разности давлений насыщения при температурах «теплой» и «холодной» межфазных поверхностей: (7)
Подставив (8)
Далее проинтегрируем левую и правую части уравнения (8) по площади поперечного сечения канала. Результат интегрирования левой части уравнения следующий: (9)
Величина (10)
Далее τ из (10) подставляется в (9), и результат интегрирования обеих частей уравнения (8) делится на площадь поперечного сечения канала. Как было отмечено ранее, свойства сверхтекучего гелия считаются постоянными. Поскольку температура Не-II по радиусу канала, очевидно, изменяется очень незначительно, то при интегрировании функцию fGM(T) также считаем постоянной величиной. Принимая допущение о том, что осредненная по площади поперечного сечения канала величина куба плотности теплового потока приблизительно равна кубу средней плотности потока (11)
В этом уравнении Динамический коэффициент вязкого трения ε при ламинарном нормальном движении определяется также как и для обычной жидкости по формуле [2]: (12)
а при турбулентном нормальном движении в диапазоне чисел Рейнольдса от 2·103 до 104 [2] – по формуле (13)
В формулах (1.2) и (13) число Рейнольдса записывается следующим образом [2]: (14)
При ламинарном течении нормального компонента из уравнения (11) с учетом соотношений (12) и (14) получаем следующую формулу для средней скорости нормального движения: (15)
Плотность теплового потока в Не-II может быть выражена формулой, приведенной в [3]: (16)
Принимая во внимание выражение (16) получаем формулу для средней скорости течения Не-II в канале при ламинарном нормальном движении и вихревом сверхтекучем движении: (17)
Легко видеть, что значение скорости (18)
где Аналогичные преобразования для турбулентного режима течения нормального компонента приводят к следующим результатам: (19)
(20)
4. РЕЗУЛЬТАТЫ: ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕФормулы для определения критического значения Нормальное движение перестает быть ламинарным, когда его скорость становится больше критической скорости (21)
Формулы (18) и (20) выведены для определения значений (22)
Таким образом, формула (18) справедлива при (23)
Соотношение (13) справедливо в диапазоне чисел Рейнольдса от 2·103 до 104. Нижняя граница этого диапазона соответствует началу развитого турбулентного режима течения нормального компонента. Очевидно, что формула (20) применима, если (24)
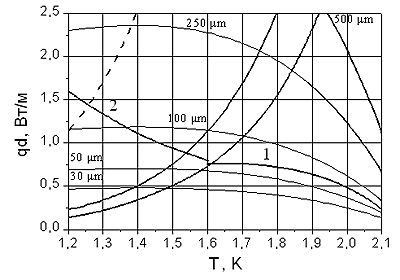
На рис. 2. показана карта режимов течения нормального компонента Не-II, построенная с помощью соотношений (23) и (24). Пространство в
Скорость (25)
Формула записана в системе СИ, число 0.0316 имеет размерность м5/4·с–1. В неподвижном Не-II реализуется противоток компонентов, поэтому (26)
Из (25), (26) и (16) при V' = 0 следует, что сверхтекучее движение является вихревым при (27)
В отличие от границ различных режимов течения нормального компонента, для сверхтекучего компонента на
Линии 1 и 2 разделяют область вихревого сверхтекучего движения на две части: ниже этих линий должно реализоваться движение сверхтекучего гелия к источнику теплоты, выше – гелий будет двигаться в направлении распространения теплового потока. Границы областей A, B, C и D получены для случая, когда 5. ЗАКЛЮЧЕНИЕПроведенные расчетные исследования стационарного движения объема сверхтекучего гелия в горизонтальном цилиндрическом капилляре при наличии продольного теплового потока показывают, что неидеальный термомеханический эффект (течение He-II к источнику теплоты при незаторможенном нормальном компоненте) возможен и в случае вихревого сверхтекучего движения. При этом режим течения нормального компонента может быть как ламинарным, так и турбулентным. Определены условия, при которых должно происходить течение He-II к источнику теплоты. Эта страница оформлена при поддержке Российского Фонда Фундаментальных Исследований (проект №08-08-00638).
СПИСОК ОБОЗНАЧЕНИЙ
Не-II – сверхтекучий гелий (гелий II); Индексы: СПИСОК ЛИТЕРАТУРЫ
1. S. W. Van Sciver. Helium Cryogenics. New York: Plenum Press. 1986. 423 p. >> * Королев П.В. Течение Не-II в горизонтальном капилляре при наличии продольного теплового потока и вихревом режиме сверхтекучего движения // Труды XVI Школы-семинара молодых ученых и специалистов под руководством академика РАН А.И. Леонтьева. В 2-х т. – М.: Издательский дом МЭИ, 2007.– Т.1.– С. 182–185. Следующая страница: Рост подогреваемой паровой полости в капилляре, заполненном Не-II
|
|
Испарение и конденсация
Пленочное кипение
Сверхтекучий гелий
Эксперименты События Библиотека Справочники Больцманиада Камерлинг-Оннес Криогениус |
|
© Криофизика.рф 2006-2021. Молекулярно-кинетическая теория. Научные публикации. Испарение и конденсация. Плёночное кипение. Сверхтекучий гелий. |
о проекте условия использования |
контакты карта сайта |
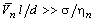 ,
,
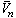 – средняя по сечению скорость течения нормального компонента He-II. Форма межфазных поверхностей в этом случае может быть любой, например, такой, какая показана на рисунке 1.
– средняя по сечению скорость течения нормального компонента He-II. Форма межфазных поверхностей в этом случае может быть любой, например, такой, какая показана на рисунке 1.
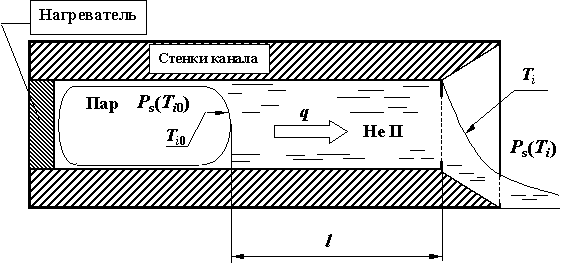
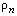 и скорость
и скорость 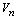 и сверхтекучего с плотностью
и сверхтекучего с плотностью 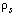 и скоростью
и скоростью 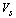 . Нормальный компонент наделен теми же свойствами, что и обычная жидкость, т.е. обладает вязкостью и переносит энтропию. Сверхтекучий компонент вязкостью не обладает и энтропию не переносит. При небольших температурных перепадах по гелию II можно принять допущение о том, что плотности
. Нормальный компонент наделен теми же свойствами, что и обычная жидкость, т.е. обладает вязкостью и переносит энтропию. Сверхтекучий компонент вязкостью не обладает и энтропию не переносит. При небольших температурных перепадах по гелию II можно принять допущение о том, что плотности 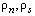 и энтропия S являются практически постоянными величинами. В этом случае, пренебрегая диссипацией и диффузионным механизмом теплопередачи в Не-II можно ограничиться записью уравнений нормального и сверхтекучего движения. Используя полуэмпирическую теорию взаимного трения Гортера-Меллинка, эти уравнения можно обобщить для случая вихревого сверхтекучего движения, когда существуют силы взаимного трения между нормальным и сверхтекучим компонентами
и энтропия S являются практически постоянными величинами. В этом случае, пренебрегая диссипацией и диффузионным механизмом теплопередачи в Не-II можно ограничиться записью уравнений нормального и сверхтекучего движения. Используя полуэмпирическую теорию взаимного трения Гортера-Меллинка, эти уравнения можно обобщить для случая вихревого сверхтекучего движения, когда существуют силы взаимного трения между нормальным и сверхтекучим компонентами 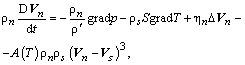
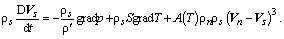
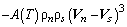 – сила взаимного трения в расчете на единицу объема, A(T)– эмпирическая величина, называемая параметром Гортера-Меллинка, зависящая от температуры.
– сила взаимного трения в расчете на единицу объема, A(T)– эмпирическая величина, называемая параметром Гортера-Меллинка, зависящая от температуры.
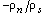 , а затем сложив левые и правые части уравнений (2) и (3) соответственно, поделив полученный результат на ρ'S, и имея в виду тот факт, что плотность теплового потока в Не-II определяется соотношением
, а затем сложив левые и правые части уравнений (2) и (3) соответственно, поделив полученный результат на ρ'S, и имея в виду тот факт, что плотность теплового потока в Не-II определяется соотношением 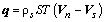 ,
,
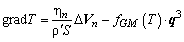 ,
,
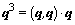 – функция Гортера-Меллинка.
– функция Гортера-Меллинка.
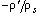 , перенеся второй и третий члены правой части налево, и учитывая соотношение (4) для случая стационарного течения Не-II, когда
, перенеся второй и третий члены правой части налево, и учитывая соотношение (4) для случая стационарного течения Не-II, когда 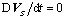 , приходим к выражению для градиента давления при вихревом сверхтекучем движении:
, приходим к выражению для градиента давления при вихревом сверхтекучем движении:
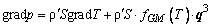 .
.
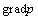 , выраженный из этого соотношения, градиенту давления из (6) получаем зависимость
, выраженный из этого соотношения, градиенту давления из (6) получаем зависимость 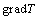 от плотности теплового потока:
от плотности теплового потока:
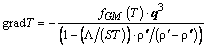 .
.
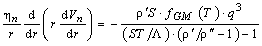 .
.
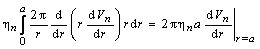 .
.
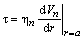 представляет собой напряжение вязкого трения нормального компонента на стенке канала, которое можно выразить через среднюю по сечению канала скорость нормального движения [2]:
представляет собой напряжение вязкого трения нормального компонента на стенке канала, которое можно выразить через среднюю по сечению канала скорость нормального движения [2]:
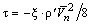 .
.
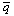 , получаем:
, получаем:
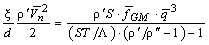 .
.
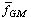 равна среднему интегральному значению функции fGM(T) в интервале температур от Тi до Тi0.
равна среднему интегральному значению функции fGM(T) в интервале температур от Тi до Тi0.
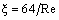 ,
,
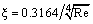 .
.
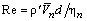 .
.
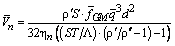
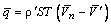 .
.
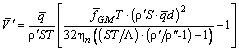 .
.
 может быть как положительным, так и отрицательным, следовательно, направление движения объема гелия II в канале должно зависеть от температуры Не-II, диаметра канала d и плотности теплового потока
может быть как положительным, так и отрицательным, следовательно, направление движения объема гелия II в канале должно зависеть от температуры Не-II, диаметра канала d и плотности теплового потока 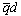 :
:
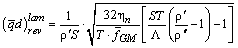 ,
,
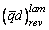 – «критическое» значение
– «критическое» значение 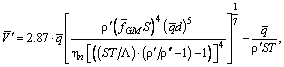
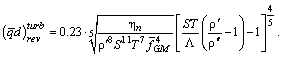
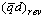 от температуры, удобно представить искомые области режимов течения в координатах
от температуры, удобно представить искомые области режимов течения в координатах 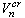 . Согласно [1] для Не-II критическое число Рейнольдса, при котором начинается переход от ламинарного режима нормального движения к турбулентному, равно 1200, следовательно, формула для
. Согласно [1] для Не-II критическое число Рейнольдса, при котором начинается переход от ламинарного режима нормального движения к турбулентному, равно 1200, следовательно, формула для 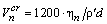 .
.
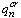 следует получить именно для случая, когда
следует получить именно для случая, когда 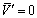 . Так как
. Так как 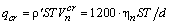 .
.
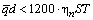 .
.
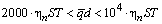 .
.
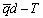 координатах делится на четыре области: A – область ламинарного режима течения; B – область переходного режима; C – область турбулентного режима при Re<104 ; D – область турбулентного режима при Re>104 .
координатах делится на четыре области: A – область ламинарного режима течения; B – область переходного режима; C – область турбулентного режима при Re<104 ; D – область турбулентного режима при Re>104 .

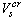 , при которой возникают вихри, формирующие, в конце концов, клубки сверхтекучей турбулентности, может быть определена по эмпирической зависимости [1]:
, при которой возникают вихри, формирующие, в конце концов, клубки сверхтекучей турбулентности, может быть определена по эмпирической зависимости [1]:
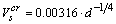 .
.
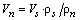 .
.
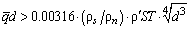 .
.