|
| Испарение и конденсация |
Пленочное кипение |
Сверхтекучий гелий |
Эксперименты | События | Библиотека |
Испарение и конденсацияПленочное кипениеСверхтекучий гелийЭксперименты События и мероприятияБиблиотека• История холода• Элементы физической кинетики• Разделение газовых смесей• Методические указания. Анализ криогенных установок• Оборудование гелиевого ожижителя Г-45• Методические указания. К практическим занятиям в криоцентре• Криогенные трубопроводы• Хранение и транпорт ожиженных газов• Основы методики проектирования криогенных установок• Вспомогательное оборудование криогенных установок• Расчет и оптимизация схем криогенных установок• Расчет низкотемпературных установок• Методика расчета схем криогенных установок (рефрижераторы и ожижители)• Методика расчета схем криогенных установок (рефрижераторы с нестационарными потоками)• Характеристики криогенных систем при работе на смесях• Механические свойства твердых тел при низких температурах• Людвиг Больцман. Лекции по теории газовСправочные данные БольцманиадаХейке Камерлинг-ОннесКриогениус |
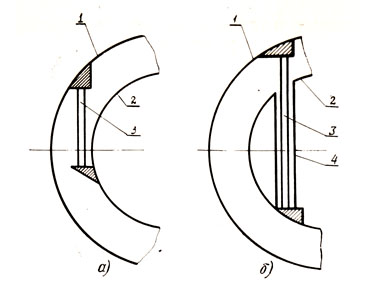
Г.И. Абрамов, В.М. Бродянский. Хранение и транспорт ожиженных газовЧасть II «ТЕПЛОВЫЕ МОСТЫ» В НИЗКОТЕМПЕРАТУРНОЙ ИЗОЛЯЦИИКонструкция криогенных систем неизбежно требует, чтобы изоляционное пространство пересекалось различными элементами, связывающими холодные и теплые зоны. К ним относятся подвески и опоры, крепящие внутреннюю оболочку относительно наружной, трубы для отвода паров криогенной жидкости, электрические вводы, коммуникации КИП и т. п. Все эти элементы являются, с точки зрения изоляции, «тепловыми мостами», т. е. по ним дополнительно передается тепловой поток. По мере повышения эффективности изоляции доля теплопритока по тепловым мостам возрастает, достигая в некоторых случаях 50% от суммарного теплопритока. Поэтому создание эффективных криогенных устройств невозможно без разработки соответствующих конструкций и способов, уменьшающих теплоприток по «тепловым мостам». 1. Подвескиа) Неохлаждаемые подвескиПодвески сосудов для ожиженных газов служат для крепления внутреннего сосуда относительно внешнего и конструктивно выполняются в виде стержней, тросов или цепей. Они крепятся к наружному кожуху и внутреннему сосуду шарнирно и работают на растяжение. Так как подвески расположены в изоляционном пространстве, то в первом приближении можно считать, что их боковая поверхность идеально теплоизолирована и что механизмом передачи тепла является «чистая» теплопроводность. Количество тепла, передаваемое по подвеске прямо пропорционально коэффициенту теплопроводности материала, площади поперечного сечения S и обратно пропорционально длине l. Поэтому подвески желательно изготовлять из материала с низким значением λ (нержавеющая сталь, текстолит, стекловолокнит марки АГ-4С и др.), одновременно стремиться уменьшить S (например, за счет применения стали марки XI8H10T повышенной прочности, полученной путем специальной обработки) и увеличивать 1. Схемы наиболее распространенных способов крепления подвесок показаны на рис. 20.
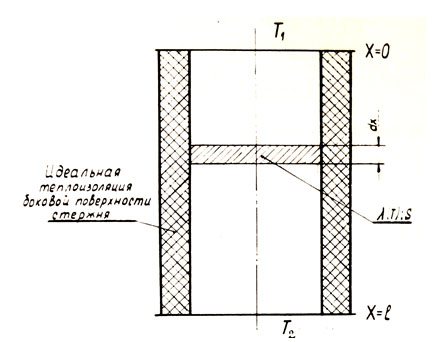
Рис. 20. Схема крепления обычных (а) и, удлиненных (б) вертикальных подвесок сосудов для ожиженных газов: 1 - наружный контейнер; 2 - внутренний сосуд; 3 - подвеска; 4 - изолирующая труба Определим теплоприток по подвеске. Задачу рассмотрим на примере стержня, боковая поверхность которого идеально изолирована (схема на рис. 21). Считаем, что температуры концов стержня заданы Т1, и Т2 и соответственно равны температурам теплой и холодной ограничивающей поверхности. Длина стержня l, площадь S поперечного сечения постоянна.
Рис. 21. К определению теплопритока по стержню Для случая постоянной величины коэффициента теплопроводности (λ=idem) уравнение теплового баланса элемента стержня длиной dх в соответствии со схемой, показанной на рис.22, запишется так: Qx = Qx+dx или по уравнению Фурье
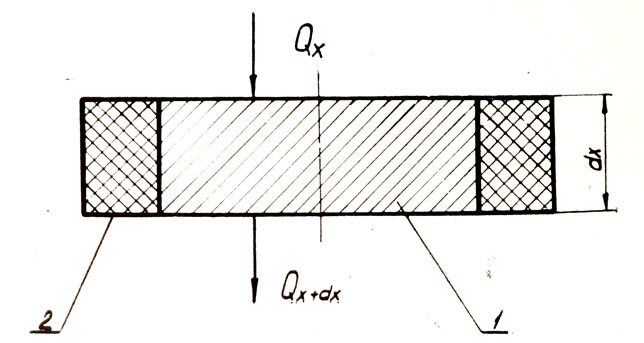
Рис. 22. Тепловой баланс для элемента стержня: 1 — выделенный элемент стержня длиной dх; 2 — изоляция Раскрывая скобки и производя сокращения, получаем:
Очевидно, что λ, S и dх ≠ 0, тогда дифференциальное уравнение теплопроводности для нашего случая будет уметь вид:
Решение (2-3) записывается в виде
где С1 и С2 – постоянные, определяемые из граничных условий.
Подставляя граничные условия в (2-4), получаем
Тогда
Тепловой поток при х = l, т. е. теплоприток по стержню
Для случая переменного значения коэффициента теплопроводности [λ=f(Т)] тепловой баланс для того же элемента стержня длиной dх в этом случае примет вид
Дифференциальное уравнение теплопроводности
Или
Разделяем переменные в (2-10) и интегрируем
Подставляем граничные условия:
Распределение температуры в стержне
или
Тепловой поток по стержню, равный
заметим, что
тогда
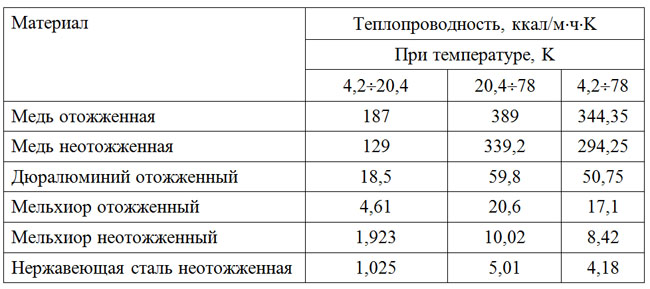
где Таблица 2-1 Теплопроводность некоторых конструкционных материалов
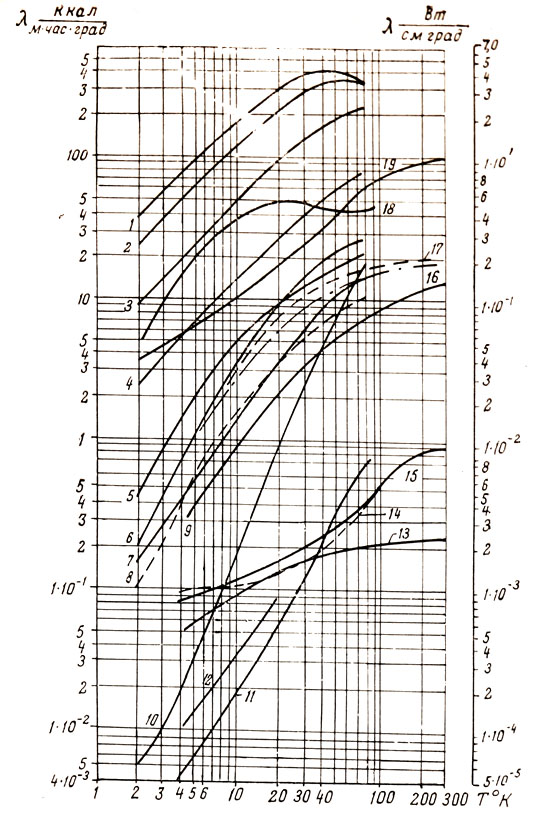
Теплопроводность технических материалов в диапазоне 2-300K представлена на рис. 23.
Рис. 23. Теплопроводность технических материалов: Расчет теплопритока по подвеске, выполненной из троса, не отличается от расчета для стрежня и проводится по формуле (2-15). В некоторых сосудах для ожиженных газов используются подвески в виде цепей. Достоинство такой конструкции связано с тем, что на пути теплового потока вводится дополнительное контактное сопротивление в месте соединения звеньев. Поэтому для вычисления теплового потока пи цепной подвеске необходимо знать термическое сопротивление контакта между звеньями цепи. Теплоприток по цепной подвеске определяется формулой
где Rц - полное термическое сопротивление цепной подвески. Rц равно сумме термических сопротивлений звеньев цепи Rзв и контактов между ними Rk
где n - число звеньев в цепи. Для определения Rц пользуются эмпирической формулой
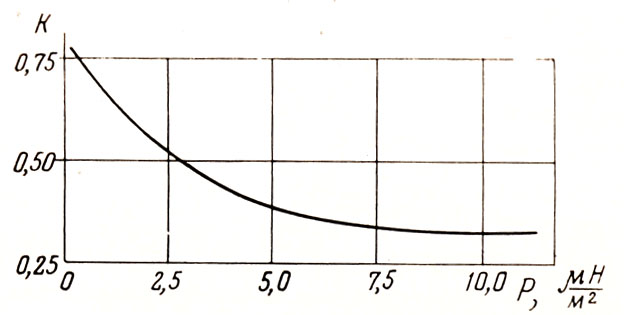
где λ - коэффициент теплопроводности материала цепи; d - диаметр прутка цепной подвески; lт - развернутая длина половины звена; k - коэффициент, зависящий от формы контактирующих тел и отношения их размеров к радиусу контактного пятна; р - удельная нагрузка на цепь, МПа. Коэффициент k может быть найден из опытных данных по термическому сопротивлению цепных подвесок. На рис. 24 приведены значения k в зависимости от удельной нагрузки на цепь, вычисленные на основе опытных данных.
Рис. 24. Зависимость теплового сопротивления между звеньями цепной подвески от удельной силы растяжения
Следующая страница: «Тепловые мосты» в низкотемпературной изоляции. Охлаждаемые подвески
|
|
Испарение и конденсация
Пленочное кипение
Сверхтекучий гелий
Эксперименты События Библиотека Справочники Больцманиада Камерлинг-Оннес Криогениус |
|
© Криофизика.рф 2006-2021. Молекулярно-кинетическая теория. Научные публикации. Испарение и конденсация. Плёночное кипение. Сверхтекучий гелий. |
о проекте условия использования |
контакты карта сайта |
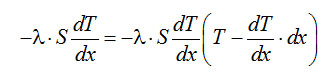 (2-1)
(2-1)
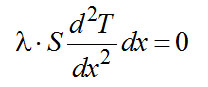 (2-2)
(2-2)
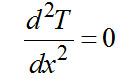 (2-3)
(2-3)
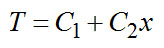 (2-4)
(2-4)
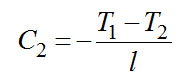 (2-5)
(2-5)
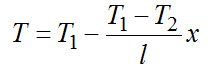 (2-6)
(2-6)
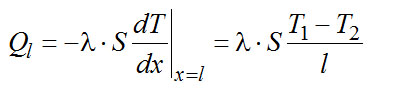 (2-7)
(2-7)
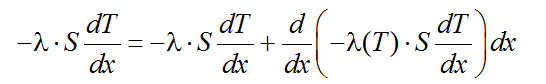 (2-8)
(2-8)
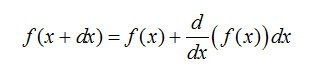
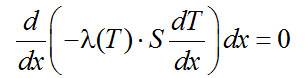 (2-9)
(2-9)
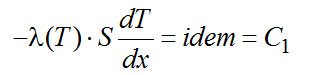 (2-10)
(2-10)
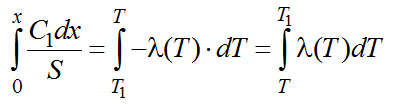 (2-11)
(2-11)
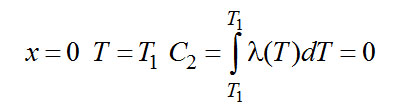 (2-12)
(2-12)
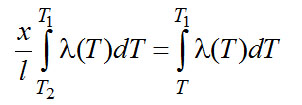 (2-13)
(2-13)
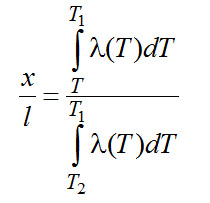 (2-13a) .
(2-13a) .
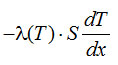 постоянен и равен С1. Поэтому теплоприток по стержню, т. е. тепловой поток на холодном конце:
постоянен и равен С1. Поэтому теплоприток по стержню, т. е. тепловой поток на холодном конце:
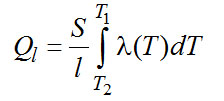 (2-14) ,
(2-14) ,
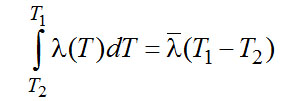
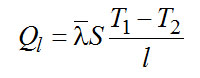 (2-15) ,
(2-15) ,
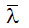 – среднеинтегральное значение коэффициента теплопроводности материала стержня в диапазоне температур Т1 – Т2. Среднеинтегральные значения коэффициента теплопроводности некоторых материалов для различных диапазонов температур приведены в табл. 2-1.
– среднеинтегральное значение коэффициента теплопроводности материала стержня в диапазоне температур Т1 – Т2. Среднеинтегральные значения коэффициента теплопроводности некоторых материалов для различных диапазонов температур приведены в табл. 2-1.
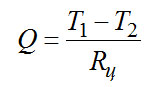 (2-16) ,
(2-16) ,
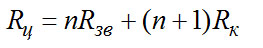 (2-17) ,
(2-17) ,
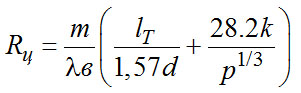 (2-18) ,
(2-18) ,