 |
| Испарение и конденсация |
Пленочное кипение |
Сверхтекучий гелий |
Эксперименты | События | Библиотека |
Испарение и конденсацияПленочное кипениеСверхтекучий гелийЭксперименты События и мероприятияБиблиотека• История холода• Элементы физической кинетики• Разделение газовых смесей• Методические указания. Анализ криогенных установок• Оборудование гелиевого ожижителя Г-45• Методические указания. К практическим занятиям в криоцентре• Криогенные трубопроводы• Хранение и транпорт ожиженных газов• Основы методики проектирования криогенных установок• Вспомогательное оборудование криогенных установок• Расчет и оптимизация схем криогенных установок• Расчет низкотемпературных установок• Методика расчета схем криогенных установок (рефрижераторы и ожижители)• Методика расчета схем криогенных установок (рефрижераторы с нестационарными потоками)• Характеристики криогенных систем при работе на смесях• Механические свойства твердых тел при низких температурах• Людвиг Больцман. Лекции по теории газовСправочные данные БольцманиадаХейке Камерлинг-ОннесКриогениус |
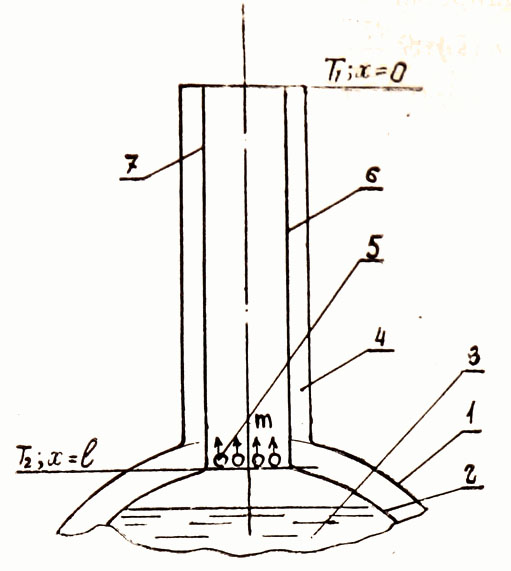
Г.И. Абрамов, В.М. Бродянский. Хранение и транспорт ожиженных газов«ТЕПЛОВЫЕ МОСТЫ» В НИЗКОТЕМПЕРАТУРНОЙ ИЗОЛЯЦИИб) Охлаждаемые подвескиПримером охлаждаемой подвески является горловика сосуда для хранения ожиженных газов. Вследствие теплопритоков из окружающей среды и тепловыделений в холодной зоне [Например от электронного устройства, находящегося в жидкости.] жидкость испаряется и пары, отводимые по горловине, охлаждают ее, снимая с внутренней боковой поверхности часть теплового потока. Схематично горловина сосуда показана на рис. 25. Определим приток тепла по горловине. Будем считать, что температуры верхнего (х=0) и нижнего (х=1) концов горловины Т1 и Т2 равны соответственно температурам окружающей среды и кипения жидкости. Так как в сечении x = l выходит насыщенный пар, то в этом сечении Тп=Ткип, где Тп - температура пара, Ткип - температура кипения жидкости.
Рис. 25. Схема горловины сосуда для хранения ожиженных газов: 1 и 2 - соответственно наружный контейнер и внутренний сосуд; 3 - кипящая жидкость; 4 - изоляция; 5- поток пара с массовым расходом m; 6 - горловина (тонкостенная трубка, обычна из нержавеющей стали); 7 - наружная труба горловины Выделяем элемент dх горловины, как показано на рис. 26, и составляем его тепловой баланс
Или
где Qиз – тепловой поток через изоляцию; Qα — тепловой поток от стенки горловины к потоку пара.
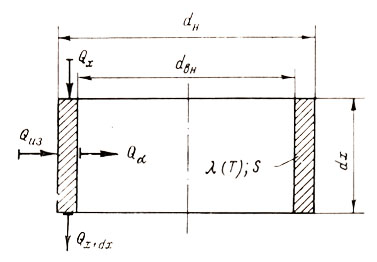
Рис. 26. Тепловой баланс элемента dх горловины При высоковакуумной изоляции
Для любой другой изоляции
где dН0 – внутренний диаметр наружной трубы горловины;
где α - среднее значение коэффициента теплоотдачи от стенки к пару. Тепловой поток в любом сечении горловины определяется по закону Фурье
Продифференцировав по х, получаем
Запишем (2-19) с учетом, например (2-20а) и (2-21):
Очевидна справедливость такого равенства:
где Приравняем (2-22) и (2-23) и продифференцируем по х
В (2-25) вместо
Для высоковакуумной изоляции выводится аналогичное уравнение с учетом (2-20). Уравнение (2-27) - дифференциальное уравнение теплопроводности трубы с теплообменом на внутренней и наружной поверхности. Для этого уравнения не может быть получено аналитического решения; оно может быть решено численно на ЭВМ для конкретного случая, т. е. для определен-ной криогенной жидкости (значение Ср), для горловины с известной геометрией (l, S, dвн0, dвн, dн0 ) выполненной из материала с определенным λ(Т).
Для третьего граничного условия необходимо знать зависимость Тп(Тст); эту зависимость можно получить из (2-25):
Численное решение (2-27) на ЭВМ даст графическую (или табличную) зависимость ТСТ, от х. Заметим, что в (2-27) два неизвестных - TCT(x) и m, причем
где Таким образом, нахождение решения (2-27) необходимо осуществлять методом последовательных приближений. Он состоит в следующем: определяется значение Решение задачи в такой постановке об определении теплопритока по горловине сосуда - весьма сложное и громоздкое. Задача значительно упрощается, если ввести некоторые допущения. Например, при условии, что коэффициент теплопроводности материала горловины не зависит от температуры и равен среднему значению а в интервале температур Т2-Т1, уравнение (2-27) приводится к более простому виду
Уравнение (2-30) является дифференциальным уравнением 3-го порядка с постоянными коэффициентами; может быть получено его аналитическое решение при выбранных ранее граничных условиях [зависимость ТП(Тст) определяется из (2-28) при Задача об определении теплопритока по горловине сосуда была решена аналитически при ?=idem и исследована экспериментально – [10]. Вычисленные и экспериментально определенные значения теплопритока для различных криогенных жидкостей и горловин из различных материалов и геометрий согласуются между собой с точностью 20-25%. Такая точность вполне допустима во многих инженерных расчетах. Для проведения более точных расчетов необходимо пользоваться уравнением (2-27). Следующая страница: 2-2. «Тепловые мосты» в низкотемпературной изоляции. Опоры
|
|
Испарение и конденсация
Пленочное кипение
Сверхтекучий гелий
Эксперименты События Библиотека Справочники Больцманиада Камерлинг-Оннес Криогениус |
|
© Криофизика.рф 2006-2021. Молекулярно-кинетическая теория. Научные публикации. Испарение и конденсация. Плёночное кипение. Сверхтекучий гелий. |
о проекте условия использования |
контакты карта сайта |
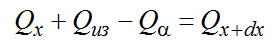
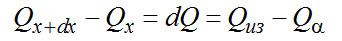 (2-19)
(2-19)
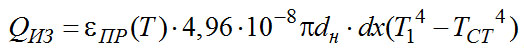 (2-20) .
(2-20) .
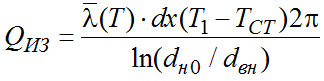 (2-20a) ,
(2-20a) ,
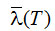 - эффективный коэффициент теплопроводности изоляции;
ТСТ - температура стенки горловины.
- эффективный коэффициент теплопроводности изоляции;
ТСТ - температура стенки горловины.
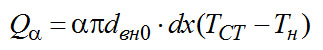 (2-21)
(2-21)
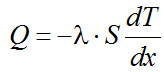
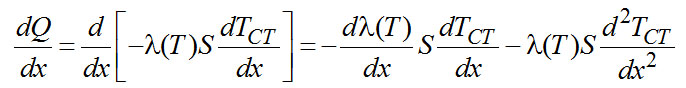 (2-22)
(2-22)
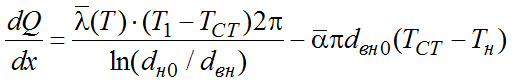 (2-23)
(2-23)
(2-23)
(2-23)
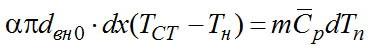 (2-24)
(2-24)
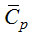 - среднее значение теплоемкости температур Т2-Т1.
- среднее значение теплоемкости температур Т2-Т1.
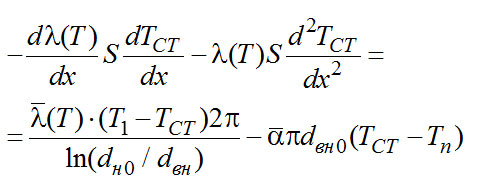 (2-25)
(2-25)
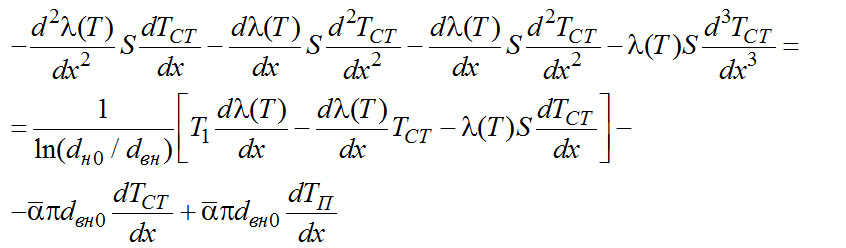 (2-26)
(2-26)
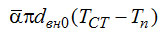 подставляем из (2-24)
подставляем из (2-24) 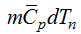 , причем значение получаем из (2-26):
, причем значение получаем из (2-26):
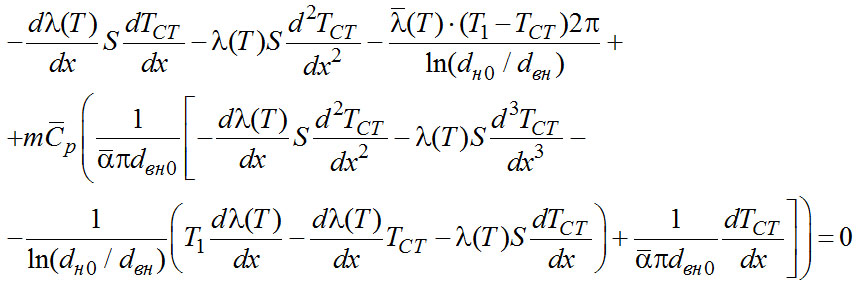 (2-27)
(2-27)
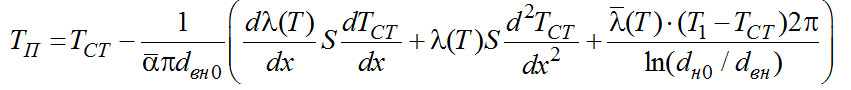 (2-28)
(2-28)
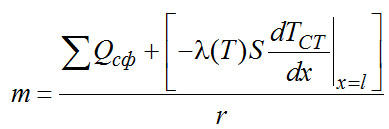 (2-29) ,
(2-29) ,
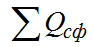 - суммарные теплопритоки к сферической (или цилиндрической, если сосуд цилиндрической формы) части сосуда; величина постоянная, зависит от температуры окружающей среды, температуры кипения жидкости, геометрических размеров сосуда, от вида изоляции и внутренних тепловыделений;
r - теплота испарения жидкости.
- суммарные теплопритоки к сферической (или цилиндрической, если сосуд цилиндрической формы) части сосуда; величина постоянная, зависит от температуры окружающей среды, температуры кипения жидкости, геометрических размеров сосуда, от вида изоляции и внутренних тепловыделений;
r - теплота испарения жидкости.
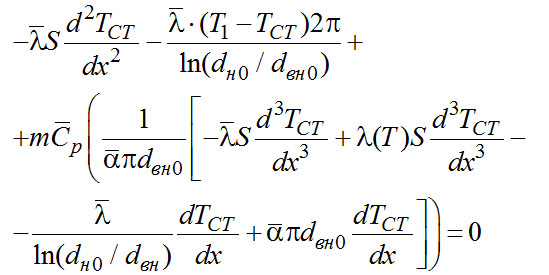 (2-30)
(2-30)
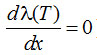 ]. Решение (2-30) получается также методом последовательных приближений с учетом (2-29).
]. Решение (2-30) получается также методом последовательных приближений с учетом (2-29).