Бродянский В.М., Калинина Е.И.
Разделение газовых смесей
Глава вторая. Минимальная работа и КПД процесса разделения
2-1. Минимальная работа разделения смеси на компоненты
Для оценки термодинамического совершенства любого процесса разделения необходимо провести сравнение его с идеальным. Идеальный процесс проходит при термодинамическом минимуме работы, который определяется ее затратой на обратимое проведение процесса разделения смеси (минимальная работа разделения).
Отношение минимальной работы разделения к реальной, затраченной в процессе, определяет эксергетический КПД процесса:
η e = lмин / ld (2-1)
Величину ld можно выразить через lмин и сумму потерь в процессе Σ d:
ld=lмин+ Σ d.
Всякое совершенствование процесса приводит к снижению Σ d, приближению ld к lмин и возрастанию η e .
Значение ld находится экспериментально или расчетным путем.
Минимальная работа разделения определяется из термодинамических положений с использованием идеальной модели процесса.
Для четкости изложения напомним определения некоторых терминов, связанных с процессами разделения.
Компонент смеси – входящее в смесь вещество определенного химического состава, содержание которого не зависит от наличия других веществ в смеси [6, 7].
Число n компонентов в смеси может быть n>2. Во многих случаях при n>3 смесь в первом приближении можно представить как бинарную, рассматривая две группы компонентов, близких по температурам кипения, как два компонента.
Фракция – смесь, полученная в процессе разделения и отличающаяся от исходной смеси повышенным содержанием одного или нескольких компонентов. В пределе фракция монет состоять из одного чистого компонента.
При разделении n-компонентной смеси можно получить n чистых компонентов, но неограниченное число фракций самого разнообразного состава.
Под процессом разделения мы будем понимать процесс получения из смеси компонентов или фракций, имеющих температуры и давления исходной смеси. Обычно температура смеси, как и продуктов разделения, принимается равной температуре окружающей среды Tсм = Ti = Tос = 293K.
Разделение может быть полным и неполным.
Полное разделение смеси – это процесс получения в чистом виде всех ее компонентов.
Неполное разделение смеси – процесс, в результате которого получается хотя бы одна фракция, не являющаяся чистым компонентом.
На практике разделение многокомпонентной смеси проводится в несколько стадий; на первой стадии получается несколько фракций. Часть из них является конечными продуктами; другая – поступает на дальнейшее разделение. Получение, например аргона из воздуха, в первой стадии сводится к получению аргонной фракции с повышенным содержанием аргона, из которой в следующей стадии вырабатывается сырой аргон, затем - аргон технический, и, в конечном итоге, – чистый аргон.
Минимальная работа разделения многокомпонентной смеси в общем виде
Для определения в общей виде минимальной работы разделения рассмотрим многокомпонентную смесь, имеющую объем Vсм. Ее состояние характеризуется термодинамическими параметрами Рсм, Тсм, Sсм, iсм, eсм. Примем также вначале, что смесь и ее компоненты – идеальные газы. Каждый из компонентов находится под своим парциальным давлением Рi, при температуре Тсм в объеме Vсм смеси.
Связь между параметрами смеси и компонентов до разделения можно по закону Дальтона записать следующим образом:
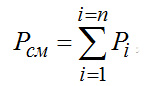 (2-2) (2-2)
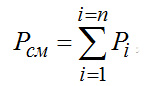 (2-3) (2-3)
Парциальное давление каждого компонента равно общему давлению, умноженному на долю компонента N в смеси.
Чтобы получить чистые компоненты при Рсм и Тсм, необходимо изотермически повысить давление каждого из компонентов от Рi до Рсм при одновременном уменьшении объема от Vi=Vсм до парциального Vk = Vсм*Ni. Определим для этих условий затрату работы и изменение параметров i, S, e в идеальной модели процесса разделения.
Такую модель можно представить в виде системы, состоящей из камеры с полупроницаемыми перегородками и компрессоров K1, K2, Ki, Kn для сжатия компонентов (рис.2-1).
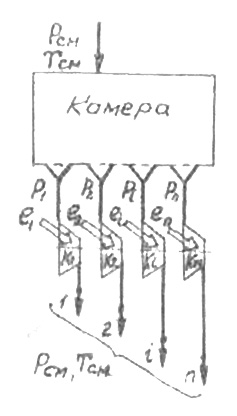
Рис. 2-1.
Смесь поступает в камеру, где давление равно Рсм и температура Тсм. Каждый компонент проходит через соответствующую полупроницаемую перегородку, которая пропускает только один компонент, и поступает в компрессор компонента с парциальным давлением Pi.
Таким образом, после камеры компоненты смеси разделены между собой и находятся под парциальными давлениями. Эта первая стадия процесса разделения проводится без затраты работы, т.к. параметры компонентов смеси остаются неизменными.
Во второй стадии проводится сжатие каждого из компонентов от Pi до Pсм при Т=Тсм. При этом необходимо в каждом компрессоре затратить работу изотермического сжатия.
Для 1 кг идеального газа:
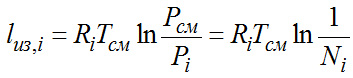 , кДж/кг; , кДж/кг;
Для 1 моля:
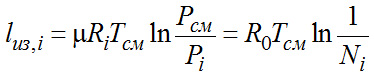 , кДж/кмоль; , кДж/кмоль;
Для Ni долей газа в смеси Li=Ni*lиз,i, кДж/кмоль смеси.
Общая затрата работы Lмин на n компонентов – минимальная работа разделения смеси – равна сумме работ изотермического сжатия всех ее компонентов:
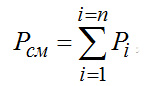 (2-4) (2-4)
Таким образом, минимальная (или идеальная) работа полного разделении идеальной газовой снеси равна суммарной работе изотермического сжатия всех ее компонентов от парциального давления до давления смеси.
Рассмотренная модель процесса разделения применима для оценки любого способа разделения, т.к. затраты работы в обратимом процессе определяются только начальным н конечным состояниями и не зависят от пути процесса.
Следующая страница: Изменение термодинамических функций в процессе разделения
| 
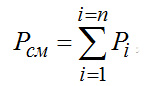 (2-2)
(2-2)

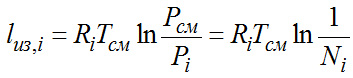 , кДж/кг;
, кДж/кг;
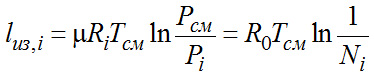 , кДж/кмоль;
, кДж/кмоль;