Бродянский В.М., Калинина Е.И.
Разделение газовых смесей
3. Процесс разделения в сдвоенной (полной) ректификационной колонне
Процессы ректификации в концентрационной и отгонной колоннах (так же, как и аналогичные процессы непрерывной противоточной конденсации и испарения) позволяют получить в каждом случае только один из компонентов в концентрированном виде. Для одновременного получения технически чистых обоих компонентов целесообразно (как это уже указывалось применительно к противоточным конденсации и испарению) объединить концентрационную и отгонную колонны.
Схема такой сдвоенной (полной) колонны в варианте с использованием конденсатора и испарители показана на рис. 3-17.
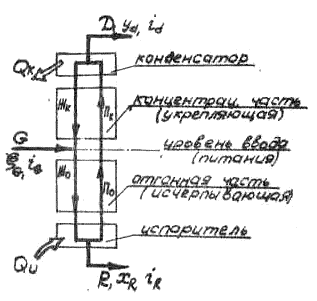
Рис. 3-17
Разделяемая смесь G подается в колонну между концентрационной и отгонной частями колонны на уровне питания.
Часть жидкости R внизу колонны и часть пара D вверху отводятся в виде продуктов разделения.
Для колонны можно записать три вида балансовых уравнений. Два из них - уравнения материального баланса по величине потоков и по количеству легкокипящего компонента в них:
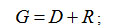 (3-23) (3-23)
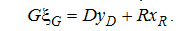 (3-24) (3-24)
Третьим является энергетический баланс
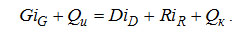 (3-25) (3-25)
или
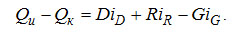 (3-25) (3-25)
Из этого уравнения следует, что при данном составе и расходах продуктом величина разности Qu - Qk = idem. Значения Qu и Qk могут изменяться в широком диапазоне, но Qu- Qk при этом остается прежней. Увеличение Qu и Qk приводит к росту энергетических затрат и потоков пара П и жидкости Ж, т.е. кратности циркуляции в колонне. Уменьшение Qu и Qk, напротив, приводит к снижению энергетических затрат на процесс. Однако нижний предел значений тепловых нагрузок не может быть меньше величин, определяемых минимальной работой разделения и собственными потерями Σdc в колонне.
Агрегатное состояние получаемых продуктов может быть любым; при этом изменяются только значения тепловых нагрузок конденсатора и испарителя. Можно, например, выводить продукт D в виде жидкости; тогда величина Qk увеличится, или R - в виде пара, что поведет к росту Qu .
При сохранении составов и количеств потоков на входе и выходе из колонны такое изменение не влияет на процесс тепломассообмена в ней.
Исходная смесь G также может подаваться на разделение в виде сухого насыщенного пара, жидкости или влажного пара. В первом случае вырастет тепловая нагрузка Qk конденсатора, во втором - испарителя Qu .
Решая совместно уравнения (3-23) и (3-24), можно показать связь между количествами продуктов R и D через концентрации всех потоков
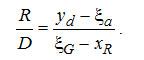
Из уравнения энергетического баланса, учитывая, что
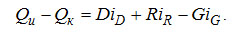
можно, сгруппировав члены с D и R, записать связь между ними через энтальпии потоков
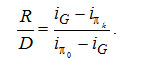
Приравнивая оба выражения для R/D , получим уравнение прямой в координатах
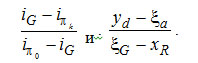 (3-26) (3-26)
Это уравнение связывает два полюса πk (i&pi k, yd) и π0 (i&pi 0, xR) , и точку, характеризующую исходную смесь G(iG,ξG) .
Все три точки πk, π0 и G лежат на одной прямой. Эта прямая называется главной полюсной линией или главной прямой колонны. В i, ξ диаграмме она разделяет области, относящиеся к концентрационной и отгонной частям (рис.3-18).
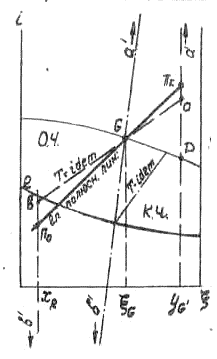
Рис. 3-18
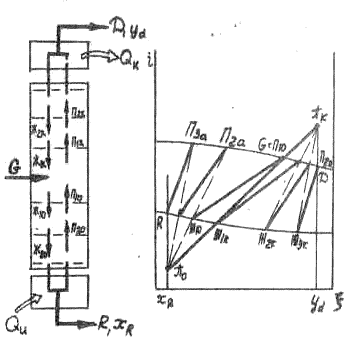
Рис. 3-19
Пользуясь i, ξ диаграммой, можно произвести расчет основных величин, характеризующих процесс ректификации и выявить некоторые его закономерности.
Расчет производятся в три этапа.
1. Составление материальных балансов колонны совместно с конденсатором н испарителем по заданным (или выбранным) концентрациям и количествам продуктов и исходной смеси.
2. Составление энергетического баланса и выбор координат полюсов.
Для этого из энергетического баланса предварительно определяется величина Qu - Qk. Абсолютные величины тепловых нагрузок испарителя и конденсатора можно определить, если задаться значением одной из величин: Qu или Qk . Это позволяет найти координаты одного из полюсов, например, π . Для нахождения другого полюса можно использовать свойства главной прямой колонны, которая должна соединять оба полюса и проходить через точку, характеризующую исходную смесь G (рис. 3-18).
Поворачивая главную конноду относительно точки G, можно совместить ее с изотермой и найти минимальные значения удельных тепловых нагрузок испарителя и конденсатора (линия а-в на рис. 3-18). При этом число тарелок n в колонне будет стремиться к бесконечности (n → ∞), а значения ΔT на тарелке питания - к нулю.
Значения Qk, мин и Qu, мин (отрезки a-D и в-R на рис. 3-18) в этом случае будут иметь минимальную величину.
Ректификация в таких предельных условиях невозможна; поэтому в реальной колонне значения qu и qk всегда должны несколько превышать qu, мин и qk, мин.
Увеличение qk и qu , как видно из диаграммы, в принципе можно вести неограниченно. При этом главная прямая колонны стремится к вертикали (линия а'–в'), а число тарелок в колонне - к минимальному (n → nмин).
Величины qk и qk в действительной колонне должны, естественно, находиться в интервале между qмакс и qмин .
Обычно для предварительных расчетов принимают qk (или qг ) ~1,2&devide;1,25 [Окончательно qи и qк определяются при технико-экономической оптимизации, которая проводится в конце первой стадии проектирования установки с учетом изменения показателей системы в целом.]
3. Определение числа идеальных тарелок в колонне.
При выбранном положении полюсов в колонне, используя метод Поншона, можно определить число идеальных тарелок nид для каждой части колонны по числу построенных изотерм. Пример соответствующего построения показан на рис. 3-19.
Из него видно, что при заданных условиях число идеальных тарелок равняется трем в концентрационной и трем в отгонной части колонны.
Число действительных тарелок nид определяется через КПД тарелки ητ [11]
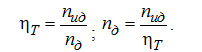 (3-27) (3-27)
Полученные данные достаточны для того, чтобы приступить к конструктивному расчету колонны. В результате этого расчета определяются скорости потоков, размеры колонны и элементов тарелок, гидравлические сопротивлении и т.д. [15].
Следующая страница: 3.4. Термодинамические особенности низкотемпературных К-И систем разделения смесей
| 

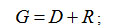 (3-23)
(3-23)
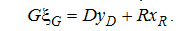 (3-24)
(3-24)
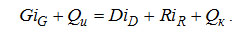 (3-25)
(3-25)
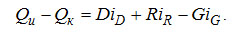 (3-25)
(3-25)
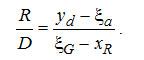
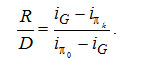
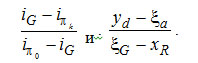 (3-26)
(3-26)


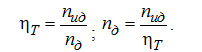 (3-27)
(3-27)