Бродянский В.М., Калинина Е.И.
Разделение газовых смесей
3.3. Ректификация бинарной смеси при T < Tос (П → Ж)
Процессы непрерывного испарения и непрерывной конденсации, как было показано выше, дают каждый в отдельности возможность разделить смесь с получением одного из компонентов в технически чистом виде, а в сочетании – и обоих компонентов одновременно.
Однако реализация этих процессов вызывает технические трудности, связанные с одновременным осуществлением внешнего теплообмена при переменной температуре и внутреннего тепломассообмена. Поэтому основное место в технике низкотемпературного разделения занял процесс ректификации, в котором эти процессы проводятся раздельно.
Внешний теплообмен полностью или частично вынесен за пределы аппарата, в котором осуществляется внутренний тепломассообмен между паром и жидкостью. [Этот процесс большей частью проводится в ректификационных колоннах: тарельчатых, насадочных и др. [1, 3, 9, 10] и реже в специальных тепломассообменных аппаратах, предназначенных для специфических условий например, невесомости) [12]. В принципе процесс ректификации не зависит от типа аппарата для внутреннего теплообмена, поэтому в дальнейшем все рассмотрение ведется применительно к колоннам. ]
Такое разделение дает возможность проводить каждый из процессов с высокой эффективностью. Наиболее распространен вариант ректификации с полным отделением этих процессов. В этого случае внутренний тепломассообмен протекает в адиабатных условиях; весь внешний теплообмен (подвод или отвод тепла) производится в специальных аппаратах (конденсаторах и испарителях). Ниже будут рассматриваться именно такие адиабатные ректификационные аппараты.
Более сложная неадиабатная ректификация, занимающая промежуточное положение между адиабатной ректификацией и непрерывными противоточными испарением и конденсацией, пока не получила распространения в силу указанных выше трудностей. Как уже отмечалось, процессы ректификации могут проводиться как при условии П>Ж, так и при Ж>П. Первый процесс (в концентрационной колонне) аналогичен непрерывной конденсации, второй (в отгонной колонне) - непрерывному испарению.
I. Процесс разделения в концентрационной колонне (П>Ж).
На рис. 3-10 показаны схемы аппарата дня непрерывной противоточной конденсации (а) и концентрационной ректификационной колонны (б).
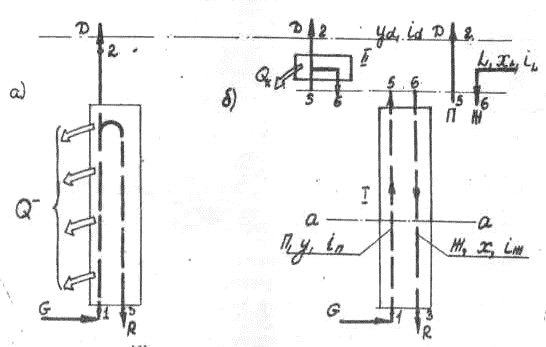
Рис. 3-10
Как в случае (а), так и в случае (б) в систему подается смесь G в виде пара и отводятся продукты разделения D и R.
Разница состоит в том, что поток жидкости Ж, стекающий навстречу поднимающемуся пару П, в случае (а) создается по всей длине аппарата при отводе тепла во всем интервале температур от Т1, до Т2, а случае (б) - вне тепломассообменного аппарата. Чаще всего жидкость получают конденсацией пара, выходящего из колонны, в специальном аппарате-конденсаторе П при самой низкой в процессе температуре (рис.3-10б, слева). В некоторых случаях жидкость L (флегма, как часто ее называют) может подаваться из других элементов общей схемы, например, из специального ожижительного контура или других разделительных колонн (рис. 3-10б, справа). В самой колонне 1 тепломассообмен П↔Ж протекает в адиабатных условиях. Рассмотрим некоторые особенности процесса в концентрационной колонне на основе ее материальных и энергетического балансов.
Воспользуемся схемой, представленной на рис. 3-10б. Верхняя часть колонны ограничена снизу произвольно выбранным сечением а-а.
Составим для этого участка балансовые уравнения.
1. Общий материальный баланс (вариант с конденсатором)
П - Ж = D = idem (3-9)
Если подача жидкости производится извне, а не после непосредственной конденсации части пара (рис. 3-10б, справа), уравнение (3-9) примет вид
П - Ж = D - L
Эти уравнения показывают, что разность потоков пара и жидкости в любом сечении колонны при заданном режиме ее работы одинакова независимо от значений П и Ж, которые могут меняться по высоте колонны. [Поскольку теплоты фазовых переходов компонентов в общем случае различны, изменение состава пара и жидкости по высоте колонны в результате внутреннего теплообмена ведет к соответствующему изменению величин Ж и П. ]
Эта разность, которая обозначается буквой π может иметь определенный физический смысл (как в первом случае, где π=D), а может быть только абстрактной расчетной величиной, как во втором случае, где нет потока, равного π.
Поскольку величина π имеет важное значение в теории ректификации (в частности, низкотемпературной) рассмотрим ее интерпретацию на i, ξ диаграмме в общем виде. На рис. 3-11 показаны точки А и В, соответствующие двум реальным потокам с расходами GА и GB, концентрациями ξА и ξB и энтальпиями iА и iB. Сложение (т.е. смешение) этих потоков в соответствии с правилом отрезков [7, 8] дает их сумму (смесь) М=А+В.
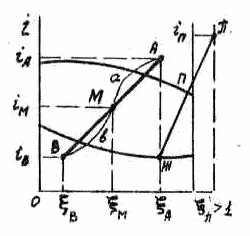
Рис. 3-11
Координаты точки М определяются длиной отрезков на прямой, соединяющей точки А и В
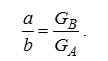 (3-10) (3-10)
Поскольку М = А + В, величина, например А, является разностью величин М и В: А=М–В (М – уменьшаемое, В – вычитаемое).
Это означает, что координаты точки А должны рассматриваться как координаты разности потоков М и В.
Эти координаты (ξA и iA) как непосредственно следует из диаграммы на рис. 3-11, могут быть найдены по двум правилам:
1) точка, отображающая разность потоков, расположена на прямой, соединяющей величины уменьшаемого и вычитаемого со стороны уменьшаемого потока;
2) расстояние точки разности потоков от точек уменьшаемого и вычитаемого потоков обратно пропорционально их величинам
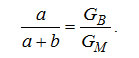
Нетрудно видеть, что величина разности потоков может характеризоваться концентрацией ξ: как ξ>1, так и ξ<0. Например, разность π пара П и жидкости Ж на диаграмме i, ξ рис. 3-11 находится за пределами диаграммы, ξπ > 1. Поскольку разность потоков - абстрактная расчетная величина, невозможность реального существования смесей с концентрацией ξ>1 или ξ<0 не мешает получать при ее использовании корректные окончательные результаты.
При дальнейшем анализе понятие разности потоков будет широко использоваться. Пользуясь этим понятием, можно уравнение (3-9) представить в виде
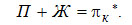
В частных случаях πk = D или πk = D - L.
2. Материальный баланс по легкокипящему компоненту
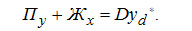 (3-11) (3-11)
При подаче жидкости извне. [Здесь и в дальнейшем величины, относящиеся к концентрационной и отгонной колоннам или частям колонны, обозначены нижними индексами К и О соответственно.]
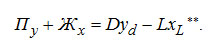 (3-11') (3-11')
Постоянную величину Пу- Жx , представляющую собой разность потоков, можно представить как постоянный поток πkξπk, который в частных случаях равен либо DyD , либо LxL
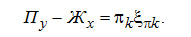 (3-12) (3-12)
Для данного режима работы колонны разность потоков ? и концентрация разности потоков являются постоянными величинами. По высоте колонны от сечения к сечению изменяются концентрации пара и жидкости (у и х), расходы пара и жидкости (П и Ж). Однако для любого сечения колонны уравнение (3-12) справедливо.
Отсюда
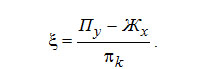 (3-12) (3-12)
3. Уравнение энергетического баланса
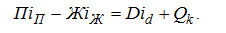 (3-13) (3-13)
или
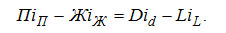 .(3-13) .(3-13)
Аналогично можно представить постоянную величину разности ПiП - ЖiЖ как некий поток πk с энтальпией iπ k. В частных случаях πkiπ k = DiD - LiL. Таким образом,
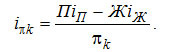 (3-14) (3-14)
Уравнение (3-14) так же, как и уравнение (3-12), действительно для любого сечения концентрационной колонны.
Уравнениям (3-12) и (3-14) в i, ξ диаграмме (рис. 3-12) удовлетворяет точка π с координатами (ξπ k ,iπ k ), лежащая на прямой аб, соединяющей точки а (y, iп) и b (x, iж), которые соответствуют состоянию пара П и жидкости Ж при подходе к данному сечению колонны. Отрезки а-πk и b-πk пропорциональны количествам жидкости и пара в этом сечении колонны.
Точка πk называется полюсом концентрационной колонны. Так как координаты точки неизменны, то состояния пара и жидкости в разных сечениях колонны можно найти на i, ξ диаграмме при пересечении прямых (лучей или коннод), проходящих через полюс колонны, с пограничными кривыми пара и жидкости, аналогично прямой ab.
На рис. 3-12 показано несколько коннод для сечений в верхней части колонны, расположенных последовательно по ее высоте.
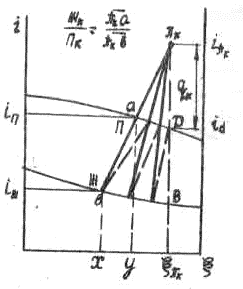
Рис. 3-12
Построение на i, ξ диаграмме, основанное на использовании понятия разности потоков, позволяет получить существенную информацию о процессах в концентрационной колонне:
1) определять для любого сечения колонны состав и расход пара П, если известны соответствующие данные для жидкости Ж (или наоборот), и соотношение между ними Ж/П в данном сечении (флегмовое отношение f);
2) находить тепловые характеристики колонны. Поскольку для схемы с конденсатором
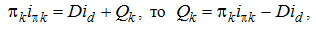 , ,
или, в удельных величинах,
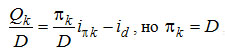
следовательно,
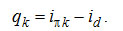 (3-15) (3-15)
На диаграмме рис. 3-12 удельная тепловая нагрузка конденсатора может быть получена, как длина отрезка πk - D . Для схемы с подводом жидкости L со стороны
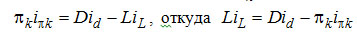
или, переходя к удельным величинам
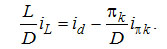
Величина L/D - это флегмовое отношение fк в верхней части колонны. Окончательно
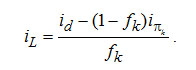 (3-16) (3-16)
Все величины, входящие в это уравнение, могут быть сняты с диаграммы i, ξ. Величина fk равна отношению отрезков D - πk и B - πk [Аналогично тому, как отношение aπk и bπk равно Ж/П в соответствующем сечении колонны.] (рис. 3-12)
3) определять число идеальных тарелок в колонне (метод Поншона) [1, 3, 7, 9, 10].
Рассмотрим произвольный участок тарельчатой колонны, показанной на рис. 3-13. Нумерация тарелок идет снизу вверх; пар и жидкость, уходящие с каждой тарелки, имеют индексы, обозначающие ее номер.
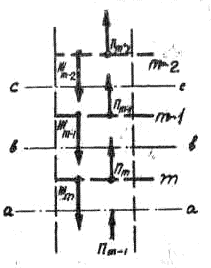
Рис. 3-13
Состояния пара П и жидкости Ж в сечениях a, b, c между тарелками изображаются в i, ξ координатах точками пересечения соответствующих коннод с пограничными кривыми пара и жидкости (рас. 3-14). Вместе с тем эти точки связаны условиями тепломассообмена на тарелках; пар и жидкость, покидающие идеальную тарелку, находятся между собой в равновесии. На диаграмме i, ξ это условие соответствует требованию, чтобы точки, изображающие состояние паря и жидкости, уходящих с одной тарелки, располагались на одной изотерме.
На рис. 3-14 показаны точки на i, ξ и Т, ξ диаграммах, характеризующие состояния пара н жидкости в сечениях и на тарелках рассматриваемого участка колонны.
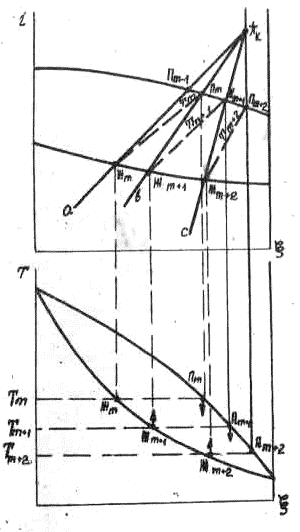
Рис. 3-14
Из диаграмм видно, что точки, соответствующие пару и жидкости, уходящим с каждой тарелки (например, Пm и Жm - с тарелки m), лежат на одной изотерме Тm (штриховая линия - Пm - Жm). Аналогично к тарелке m+1 относится изотерма Тm+1 (линия - Пm+1 и Жm+1).
На базе этого построения можно найти количество идеальных тарелок в концентрационной части колонны, проводя последовательно конноды и изотермы. Число изотерм будет равно числу идеальных тарелок. Граничные конноды определяются составами входящих в колонну и выходящих из нее продуктов.
Следующая страница: Процесс разделения в отгонной колонне
| 


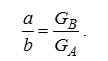 (3-10)
(3-10)
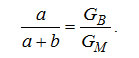
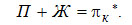
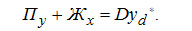 (3-11)
(3-11)
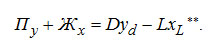 (3-11')
(3-11')
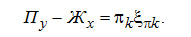 (3-12)
(3-12)
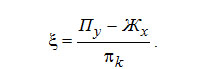 (3-12)
(3-12)
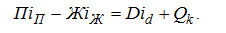 (3-13)
(3-13)
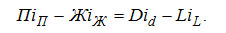 .(3-13)
.(3-13)
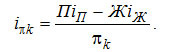 (3-14)
(3-14)

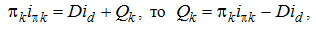 ,
,
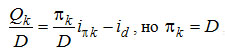
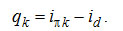 (3-15)
(3-15)
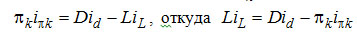
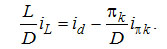
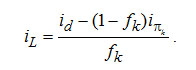 (3-16)
(3-16)

