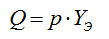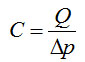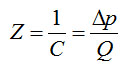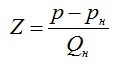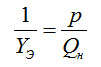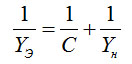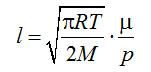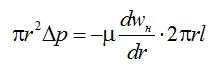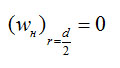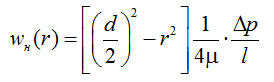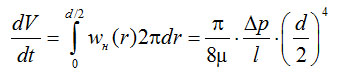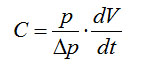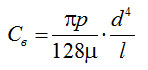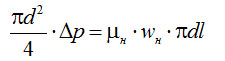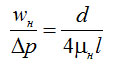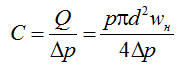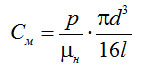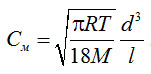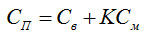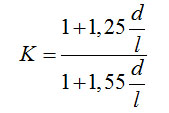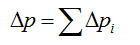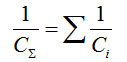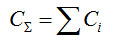Вспомогательное оборудование криогенных установок
Грачев А.Б., Боярский М.Ю., Савинова Н.М.

§5. Основы расчета вакуумных систем

1. Обеспечение заданного давления в системе

Для поддержания в системе заданного вакуума необходимо, чтобы поток газа, удаляемого из системы, был равен газовыделениям. Как отмечалось ранее, величину потока газа, отводимого из системы, можно определить по уравнению

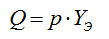
(4-5)

где Y_Э – эффективная быстрота откачки системы.

Величина Y_Э определяется как быстротой откачки насоса, так и пропускной способностью газового тракта, который соединяет систему с насосом. При этом пропускная способность – С определяется как отношение величины потока газа Q к разности давлений Δp на концах газового тракта

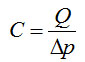
(4-6)

Величина, обратная пропускной способности, называется сопротивлением

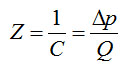
(4-7)

Пусть откачка системы производится насосом с быстротой откачки через коммуникацию, сопротивление которой

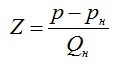
(4-8)

где р и р_н – давление в системе и на входе насоса соответственно.

Эффективная быстрота откачки может быть определена из уравнения

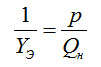
(4-9)

Подставляя в (4-9) значение p/Q_н из (4-8), найдем

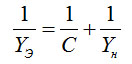
(4-10)

Из уравнения (4-10) следует, что эффективная быстрота откачки системы, соединенной с насосом коммуникацией, имеющей ограниченную пропускную способность, всегда меньше быстроты откачки насосов. Пропускная способность коммуникаций определяется длиной и формой каналов, а также режимом течения газа.

Характер большинства физических явлений в вакууме зависит от соотношения взаимных соударений молекул и соударений молекул с поверхностями, ограничивающими вакуумируемый объем. Если длина свободного пробега молекул l существенно меньше характерного размера системы d, например диаметра трубопровода, то преобладают столкновения молекул между собой. В этом случае поток газа рассматривают как сплошную среду и режим течения называют вязкостным. При уменьшении концентрации молекул в единице объема длина их свободного пробега l увеличивается и для случая, когда l > d, преобладают столкновения молекул со стенками. Такой режим течения газа называют молекулярным.

Отношение длины свободного пробега l к характерному размеру системы d называют критерием Кнудсена Kn=l/d. По величине этого критерия может быть определен режим течения газа: Kn < 0,01 – вязкостный, 0,01 < Kn < 1 – переходный, Kn > 1 – молекулярный.

Величина l определяется на основе молекулярно-кинетической теории газов [9] по уравнению

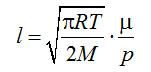
(4-11)

где μ - вязкость, R – индивидуальная газовая постоянная, M – молекулярная масса.

Установив вид режима течения газа, можно рассчитать пропускную способность коммуникация для каналов относительно простой формы. Например, для длинного трубопровода пропускная способность может быть определена из баланса сил трения и сил давления на торцевые поверхности для цилиндрического элемента газа.

Для вязкостного режима течения рассмотрим элементарный цилиндрический элемент газа длиной l и радиусом d_r, находящийся в трубопроводе с диаметром d. Баланс сил для этого элемента запишем в виде:

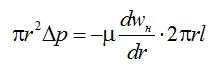
(4-12)

где Δp – разность давлений на концах трубопровода длиной l, w_н – скорость потока в осевом направлении.

Интегрируя уравнение (4-12) при условии

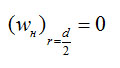
найдем радиальное распределение скорости

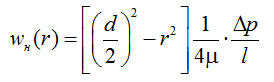
(4-13)

Определив объемный расход газа через трубопровод как

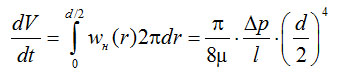
(4-14)

и учитывая из (4-2) и (4-5), что

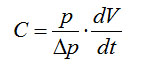
(4-15)

найдем пропускную способность трубопровода в вязкостном режиме

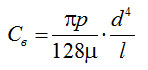
(4-16)

При молекулярном режиме течения скорость в осевом направлении w_н по сечению неизменена, поскольку силы вязкости отсутствуют. Для расчета пропускной способности C_м в этом случае приравниваем силы давления на торцевые поверхности элемента радиусом r=d/2 и силы молекулярного трения о поверхность трубы

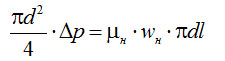
(4-17)

где μ_н – коэффициент молекулярного трения [7].

Из (4-17) определим величину w_н/Δp :

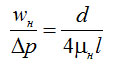
(4-18)

Учитывая, что пропускная способность

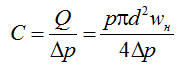
(4-19)
,

Из (4-18) и (4-19) найдем

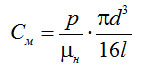
(4-20)

Используя для p и μ_н соотношения, полученные на основе молекулярно-кинетической теории [9], получим после преобразований

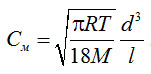
(4-21)

При расчете пропускной способности для переходного режима течения необходимо учитывать как вязкостное, так и молекулярное течения. Кнудсен предложил полуимперическое уравнение для расчета пропускной способности трубы C_n в переходном режиме [14]

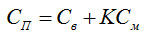
(4-22)

где

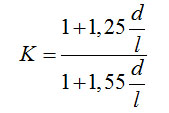
(4-23)

Здесь длина свободного пробега молекул l должна рассчитываться при среднем давлении в трубопроводе.

Сопоставление уравнений (4-16) и (4-21) показывает, что зависимость пропускной способности трубы от диаметра в молекулярном режиме слабее, чем в вязкостном. Кроме того, величина C_м в отличие от C_в не зависит от давления. Для легких газов величина C_м больше, чем для тяжелых. Уравнения, определяющие пропускную способность различных коммуникаций, приводятся в специальной и справочной литературе [10, 7, 15]. Сложные коммуникации можно представить в виде последовательного или параллельного соединения простых участков, пропускная способность которых определяется по соответствующим формулам.

При последовательном соединении величина потока на каждом участке неизменна Q=idem. Кроме того, разность давлений на концах коммуникаций можно определить по уравнению

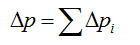
(4-24)

где Δp_i - разность давлений на каждом участке. Учитывая, что Δp = Q/C_Σ и Δp_i = Q/C_i, найдем

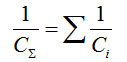
(4-25)

При параллельном соединении участков разность давлений на каждом участке одинаковая Δp=Δp_i=item, а поток Q газа через систему равен сумме потоков через каждый участок. В связи с этим

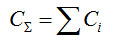
(4-26)

Таким образом, зная геометрическую характеристику системы, можно определить ее пропускную способность. При известных пропускной способности коммуникаций и быстроте откачки насоса можно рассчитывать эффективную быстроту откачки системы и поток газа, удаляемый из системы. Равновесное давление установится в тот момент, когда откачиваемый поток будет равен потокам газовыделения и натекания.

Следующая страница: 4.5.2. Определение времени откачки системы