Бродянский В.М., Калинина Е.И.
Разделение газовых смесей
Примеры разделения смеси
Рассмотрим два примера разделения смеси состава ξсм при давлении Рос и температуре Тос. Соответствующая изотерма 1-0-2 показана на е, ξ - диаграмме.
1. Смесь разделается на чистые О2 (ξ=0) и N2 (ξ=1) .
В этом случае минимальная работа разделения равна Δe3-0 на 1 кг разделяемого продукта. Если, например, нужно найти величину этой работы, отнесенную к 1 кг продукта О2, то необходимо из любой точки, находящейся на ординате ξ=1 (например, из точки 7), провести два луча, проходящих через точки 3 и 0. Расстояние между точками пересечения этих лучей на ординате продукта О2 (ξ=0) определит искомую величину работы на 1 кг продукта О2.
В рассматриваемом примере показаны лучи 7-11 и 8-7. Искомая величина работы равна е11–е8.
2. Смесь разделяется на продукты K и А (точки 4 и 5). Величина минимальной работы на 1 кг разделяемой смеси равна Δe0-6. Работа, отнесенная к 1 кг продукта А, определяется посредством такого же построения, как в предыдущей примере, и равна величине Δe10-12.
Особенности e, ξ - диаграммы воздуха.
e, ξ - диаграмма воздуха имеет некоторые особенности. Они связаны с тем, что воздух является окружающей средой и его нулевая эксергия е0 =0.
Рассмотрим нижнюю часть e, ξ -диаграммы для воздуха.
Как было показано выше, при понижении давления изотерма частично или полностью опускается ниже горизонтали е=0. Это означает, что при соответствующем давлении эксергия одного из компонентов может быть равной нулю. Так, изотерма 3-4 на рис. 2-11 соответствует давлению, при котором эксергия азота равна нулю, а изотерма 5-6 – давлению, при котором нулю равна эксергия кислорода.
Легко показать, что в первой случае давление равно 0,79 кгс/см2 – парциальному давлению азота в воздухе, а во второй – 0,21 кгс/см2 – парциальному давлению кислорода.
Действительно, по формуле (2-8) эксергия е0 1 м3 из данного чистого компонента воздуха при Тос=293K и давлении, равном 1 кгс/см2, составит
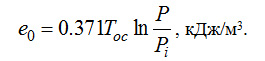 (2-9) (2-9)
При давлении Р=0,79 кгс/см2 величина e должна вычисляться по той же формуле (2-9), но в числителе дроби под знаком ln должна стоять вместо единицы величина 0,79. Поскольку значение Рi для азота в воздухе тоже составляет 0,79, то ln(0,79/0,79)=0 и е =0.
Аналогично для кислорода Рi=0,21, величина ln(0,21/0,21)=0 и эксергия соответственно равна 0.
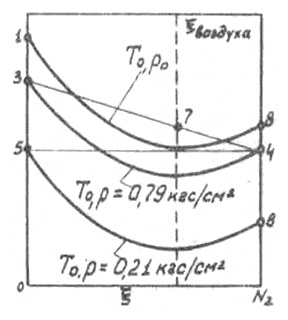
Рис. 2-11.
Физический смысл значения эксергии, равного нулю, состоит в том, что для получения любого чистого компонента воздуха при парциальном давлении в идеальном случае не нужно никакой затраты работы, так как парциальное давление компонента в смеси и давление его в чистом виде равны.
Если эксергия или равная ей минимальная работа получения одного из компонентов равна нулю, то работа разделения будет определяться только эксергией другого компонента. Так, работа выделения кислорода при Pос и Tос из воздуха, находящегося при тех же параметрах, отнесенная к единице расхода кислорода, как видно из рис. 2-10, равна его нулевой эксергии. Отнесенная к единице расхода воздуха, эта величина равна эксергии в точке 7 (рис.2-11).
Таким образом, как уже указывалось, принципиально возможно выделить из воздуха любой компонент с затратой работы, равной его нулевой эксергии, оставляя смесь других компонентов при парциальном давлении. При полной разделении смеси все получаемые компоненты доводятся до давления Pос и минимальная работа равна сумме нулевых эксергий получаемых компонентов.
Необходимо еще раз подчеркнуть, что обратимое выделение компонентов или их смесей без получения других продуктов разделения принципиально возможно только в том случае, если сырьем служит атмосферный воздух (или другая смесь, количество которой практически неограниченно по сравнению с количеством извлекаемого продукта).
Следующая страница: 3.1. Общая характеристика и классификация низкотемпературных процессов разделения
| 
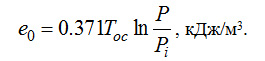 (2-9)
(2-9)
